[Construction
de l'adjoint]
[Directions
propres de l'adjoint]
[Construction d'endomorphismes
auto-adjoints] [Directions
propres des auto-adjoints] [Cas
particulier de f* o f]
Soit s une symétrie vectorielle. Alors s est un endomorphisme auto-adjoint si et seulement si c'est une symétrie orthogonale.
|
|
|
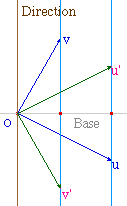
La construction d'une symétrie vectorielle avec Cabri est tout simplement celle d'une symétrie oblique : le milieu des extrémités des vecteurs u et u' appartient à la base de la symétrie (direction propre associée à la valeur propre 1).
|
|
|
 |
|