Plan vectoriel euclidien
Directions propres des
endomorphismes auto-adjoints

 

 

   [Construction de l'adjoint] [Directions propres de l'adjoint] [Adjoint et symétrie (vers auto-adjoint]
[Construction d'endomorphismes auto-adjoints] [Cas particulier de f* o f]

  [Groupe linéaire GL2(R)] [Réduction des endomorphismes]

 

On sait qu'un endomorphisme est dit auto-adjoint ou symétrique quand il est égal à son adjoint, autrement dit quand f* = f.

Les endomorphismes symétriques jouent un rôle important en algébre linéaire. Bien-sûr en dimension 2 l'intérêt est limité. Nous illustrerons toutefois le cas particulier du théorème suivant :

Un endomorphisme symétrique est diagonalisable dans une base orthogonale de vecteurs propres.

Pour réaliser les figures, on a besoin deCharger la macro CnstAAdj.mac (1.1.5) ou AutoAdj8.mac (1.1.8) qui construit un endomorphisme auto-adjoint.

Rappel sur cette macro : Ne pas oublier qu'elle construit un vecteur v' parmi de nombreux possibles. Si le vecteur construit paraît trop grand, on pensera à le modifier.

On utilisera aussi la macro DirProp.mac qui construit les directions propres d'un endomorphisme.

 

Illustration du théorème

Lancer la figure DPAAdj1.fig (1.1.5) ou DPAAdj8.fig (1.1.8) ci-dessus.

Il est intéressant d'observer plus avant la rotation des directions propres quand v' de déplace selon son degré de liberté (selon une direction orthogonale à u). Par exemple quand devient colinéaire à v, on retrouve naturellement une direction propre. De même, on ne sera pas surpris, à priori de retrouver aussi une direction propre quand v' devient colinéaire à u' (illustration 2) car dans ce cas, l'endomorphisme auto-adjoint n'est pas bijectif, l'autre direction propre étant son noyau.

Détail sur ce dernier cas : on a construit w', l'image d'un vecteur w.

À propos de la preuve du résultat

 

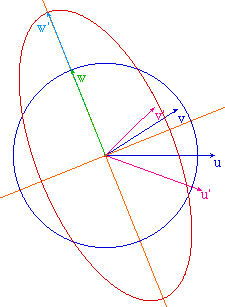
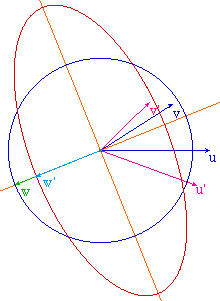
Parmi les différentes façons de montrer qu'un endomorphisme auto-adjoint est diagonalisable, et qu'il l'est dans une base orthogonale de vecteurs propres, une des méthodes consiste à trouver une valeur propre (c'est à priori la difficulté dans R) comme étant la valeur du Max ||f(x)|| pour x parcourant la sphère unité. On montre que ce Max est atteint sur un vecteur propre, puis que c'est une valeur propre (et c'est alors celle de plus grand module). On poursuit dans l'orthogonal par récurrence. C'est par exemple la méthode utilisée dans le traité d'Arnaudies - Fraysse (Tome 4 p 110).

Il est intéressant d'accompagner cette preuve d'une illustration avec Cabri comme ci-contre.

DPAAdj2.fig (1.1.5) ou PrAdj118.fig (1.1.8)

 

Plaçons w tel que w et w' soient colinéaires ... et l'on retrouve l'extremum ...

 

   [Construction de l'adjoint] [Directions propres de l'adjoint] [Adjoint et symétrie (vers auto-adjoint]
[Construction d'endomorphismes auto-adjoints] [Cas particulier de f* o f]

  [Groupe linéaire GL2(R)] [Réduction des endomorphismes]

 

Menu général