[Construction
de l'adjoint] [Adjoint et
symétrie (vers auto-adjoint]
[Construction d'endomorphismes
auto-adjoints] [Directions
propres des auto-adjoints] [Cas
particulier de f* o f]
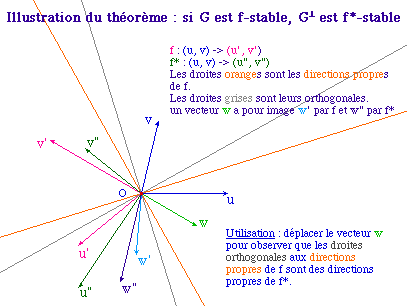
Si un endomorphisme a (seulement) deux directions propres distinctes, son adjoint a aussi deux directions propres distinctes qui sont les directions orthogonales des premières.

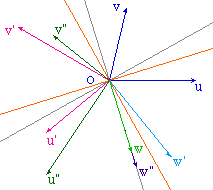
Illustration dans le cas
d'une |
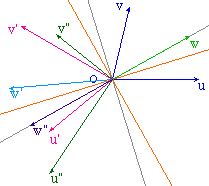
Illustration dans le cas
d'une |
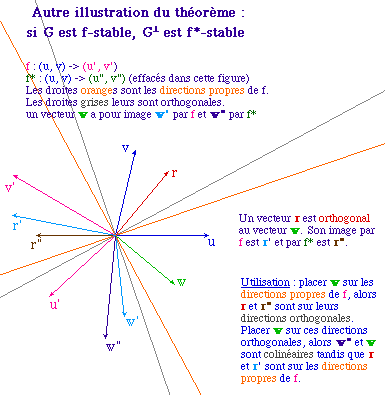
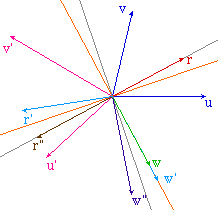
Cas où w est vecteur propre
de f
|
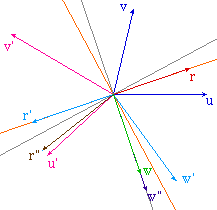
Cas où w est vecteur propre
de f* |
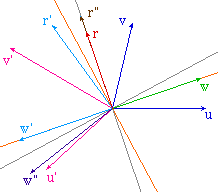
Cas où w est vecteur propre
de f |
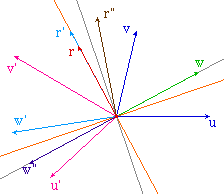
Cas où w est vecteur propre
de f* |