Les figures de cette page sont compatibles Cabri 1.1.5 et 1.1.8.
|
|
Aprés avoir construit la trace et le déterminant d'une application linéaire, nous sommes en mesure de construire ses valeurs propres puisque, en dimension 2, elles sont entièrement déterminées par la trace et le déterminant : ce sont les racines du polynôme X2 - tr f X + det f.
La trace et le déterminant étant exprimé dans le même repère (O, u) - voir pages précédentes - la construction va être aisée. On se propose ici d'utiliser celle dite de l'orthogone de Lill.
|
|
|
L'orthogone de Lill est une construction présente dans plusieurs ouvrages scolaires (dont l'IREM de Strasbourg). On se reportera à l'activité TI 92 de Nathalie Aymé pour une présentation en classe et les preuves proposées en 1°S.(image de la page de Nathalie) |
|
|
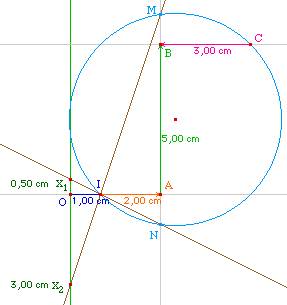
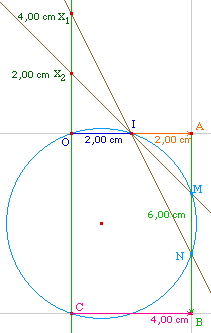
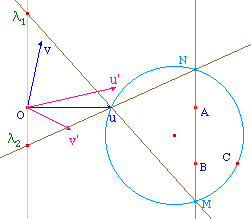
Rappelons les résultats pratiques de cette construction : Dans un repère - euclidien - où OI = 1, on construit, en mesure algébrique, en abscisse IA = 2, en ordonnée AB = b, et parallèlement à l'axe des abscisses, BC = -c (attention au signe). La construction de Lill donne, en ordonnées, les solutions de l'équation aX2 + bX + c = 0.Le cercle de diamètre [IC] coupe - éventuellement - la droite (AB) en M et N. Les droites (IM) et (IN) coupent l'axe des ordonnées en deux points dont les ordonnées sont les racines du polynômes.Par exemple ci-dessus, on lit que les solutions de l'équation 2X2 + 5X - 3 = 0 sont les nombres 1/2 et -3.
|
 |
L'intérêt de cette construction, outre sa simplicité bien connue, est ici son caractère homothétique : en réalité, il est immédiat de voir que si les coefficients sont exprimés dans une unité donnée, les solutions sont aussi exprimées dans cet unité. Ainsi par exemple les solutions de l'équation X2 - 3X + 2 = 0 sont 1 et 2.L'illustration ci-contre montre bien que l'on a ces solutions dans un repère d'unité 2 cm.En particulier, nous allons pouvoir construire ainsi les valeurs propres d'un endomorphismes, dans l'unité (O, u) dans laquelle on a construit la trace et le déterminant. |
Charger
les macros DetAL.mac
et TraceAL.mac.|
|
A est tel que uA = Ou (en vecteur) car le coefficient a est égal à 1.On place ensuite en ordonnée K tel que OK = - O tr (en mesure algébrique). En effet, le polynôme étudié est X2 - tr f X + det f. Ensuite on construit B tel que AB = OK en mesure algébrique.Pour construire C il suffit de translater B du vecteur d'origine det d'extrémité O.Remarque importante : pour la suite de la construction on évitera d'utiliser la droite (AB) pour préférer la perpendiculaire à (O u) en A. En effet, en prenant la droite (AB) la construction disparaît quand la trace de l'endomorphisme est nulle, car alors A = B. Pour la dimension 2, cela exclurait l'utilisation pour les symétries vectorielles, ce qui serait dommage. |
 |
On se place dans le cas où le cercle de diamètre [uC] coupe la droite (AB). Soient M et N leurs intersections. Les droites (uM) et (uN) recoupent l'axe des ordonnées en les deux solutions.Il suffit de les reporter sur (Ou) , comme ci-dessous : |
Lancer
la figure ValProp2.fig
précédente de construction des (éventuelles)
valeurs propres ou ValProp3.fig
sa version "nettoyée" illustrée ci-dessous.
Charger
la macro ValProp.mac
associée : les valeurs propres apparaissent ... si elles
existent.
Menu
général
