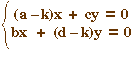
Ainsi les directions propres sont données par le rapport
Les figures de cette page sont compatibles Cabri 1.1.5 et 1.1.8.
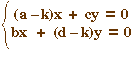
|
|
Une fois les valeurs propres disponibles, il suffit de construire c en abscisse et k-a en ordonnée pour chacune des deux valeurs propres :La valeur propre k se projette sur l'axe (Ov) en kv selon la direction (uv), de même a se projette en av. La translation de vecteur d'origine av d'extrémité O envoie kv en le point k-a. Le point D de coordonnées (c, k-a) est donc un élément de la direction propre associée à k. |
|
|
On fait de même pour la seconde valeur propre. Il est inutile d'utiliser une macro partielle, de nombreux objets étant déjà construits : la droite (OD') est la seconde direction propre de l'endomorphismeRemarque : la construction du point c a été effectuée à des fins d'explication, mais le lecteur se rendra compte qu'elle est totalement inutile.
|
|
|
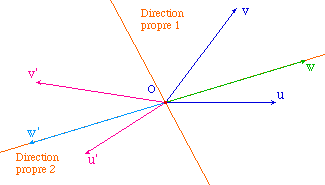
On se donne une application linéaire qui a effectivement des directions propres et de plus un vecteur w d'image w', obtenue par la macro ImVectAL.mac.
|
|
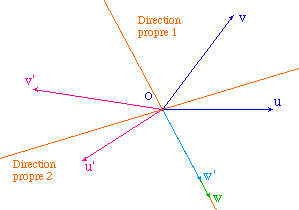
Cas d'une valeur propre positive |
|
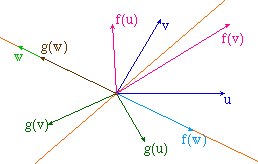 |
Reprenons la figure GLComm2.fig (1.1.5) ou GLComm3.fig (1.1.8) ou des applications f et g commutantes. Et appliquons lui la macro de directions propres de f :
|