[Construction
de l'adjoint] [Directions
propres de l'adjoint] [Adjoint et
symétrie (vers auto-adjoint]
[Directions propres des
auto-adjoints] [Cas
particulier de f* o f]
|
|
Comme indiqué dans la présentation, on construit j orthogonal à u et de même norme.u' a pour coordonnées (a, b) dans la base (u, j). On reporte b en abscisse (car b = c d'aprés la remarque). j' est un vecteur dont l'extrémité est sur la droite passant par ce point et de direction j. ON a donc un degré de liberté (cofficient d indéterminé) pour le vecteur j'.L'endomorphisme qui envoie (u, j) sur (u', j') est auto-dajoint. |
|
|
L'application de la macro ImVectAL.mac sur un vecteur v quelconque donne l'image v' tel que f : (u,v) -> (u', v') soit auto-adjoint.Le degré de liberté (coefficient d) sur j' induit un degré de liberté sur v' : quand l'extrémité du vecteur j' décrit la droite dirigée par j, l'extrémité du vecteur v' décrit une droite dirigée elle aussi par j.
|
|
|
Pour le vecteur j'0 on peut prendre tout simplement celui colinéaire au vecteur de base u. Dans la figure ci-contre l'extrémité du vecteur v' est un point sur objet de la droite passant par l'extrémité de v'0, et direction j.Par construction, l'endomorphisme qui envoie la base (u, v) sur la base (u', v') est auto-adjoint.
|
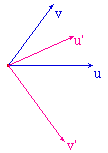
Avant l'application de la macro Adjoint
|
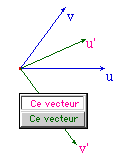
Aprés l'application de la macro (2° vecteur) |
|
|
On peut aussi se souvenir que cette macro Adjoint donne une désignation à l'image du premier vecteur montré, pour distinguer f*(u) et f*(v) :Pour le fun, on peut
|