|
|
On montre alors qu'il existe une base dans laquelle la matrice de l'application peut s'écrire avec des termes tous nuls sur la diagonale. |
[Macros de base] [Illustration : commutant] [Trace] [Déterminant]
|
|
On montre alors qu'il existe une base dans laquelle la matrice de l'application peut s'écrire avec des termes tous nuls sur la diagonale. |
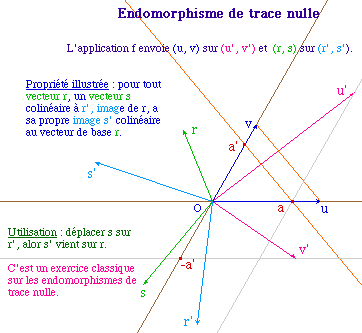
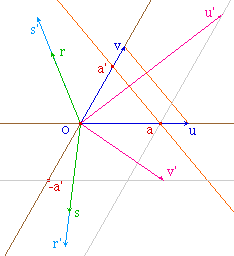
Comme dans les pages précédentes, on écrira indifféremment "le vecteur Oa" ou encore "le repère (O, a)" par abus de notation évident.
|
|
Si a est l'abscisse de u' dans (u, v), on construit le point a' sur (Ov) d'ordonnée a dans (O, v), et le point d'ordonnée -a'.La droite passant par ce point parallèle à (Ou) est l'ensemble des points v' tels que l'application linéaire qui envoie (u, v) sur (u', v') soit de trace nulle. |
La
figure GLTrNul1.fig
(les deux versions de
Cabri)
[Macros de base] [Illustration : commutant] [Trace] [Déterminant]
Menu
général
