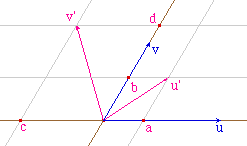
 |
Si u' et v' ont pour coordonnées u'(a, b) et v'(c, d) dans la base (u, v), le déterminant de l'application linéaire est le nombre ad-bc.
|
[Macros de base] [Illustration : commutant] [Trace] [Illustration : endomorphisme de trace nulle]
Comme dans la page précédente, on écrira indifféremment "le vecteur Oa" ou encore "le repère (O, a)" par abus de notation évident.
|
|
Si u' et v' ont pour coordonnées u'(a, b) et v'(c, d) dans la base (u, v), le déterminant de l'application linéaire est le nombre ad-bc.
|
 |
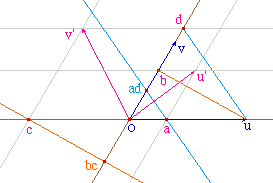a. Construction des facteurs.La parallèle à (ud) passant par a donnele produit ad sur (Ov).De même la parallèle à (ub) passant par c donne le produit bc. |
|
|
b. Soustraction des termes, passage sur (Ou).Pour retrancher le produit bc à ad, on translate le point en ad du vecteur d'origine bc d'extrémité O. On obtient ainsi le point d'ordonnée ad-bc.La parallèle à (uv) passant par ce point coupe (Ou) au point d'abscisse le déterminant de l'application linéaire, exprimée dans le repère (O, u).
|
La macro DetAL.mac
associée : objets initiaux u, v, u', v', objet final le point
"det".
|
|
Pour réaliser la figure suivante, il est utile de disposer de la macro construisant l'image d'une base par une application linéaire.
|
|
|
La même démarche peut être utilisée pour illustrer le théorème du produit des déterminants. Dans la figure suivante, on a construit le déterminant de f sur u, celui de g sur v (inverser les rôles de u et v dans l'application de la macro) et celui de fog sur u. Det f sur u et det g sur v permet de construire le produit det f. det g sur v par la parallèle à (u det g) passant par det f.La vérification d'égalité se résume à vérifier que la droite passant par les deux points construits - la droite (det fog det f. det g) est parallèle à (uv).
|
Menu
général
