[Macros de base] [Trace] [Déterminant] [Illustration : endomorphisme de trace nulle]
|
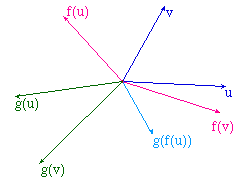
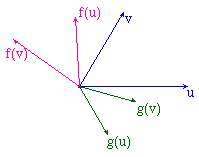
Soit f une application linéaire, définie par son image (u', v') = (f(u), f(v)) d'une base (u, v). Pour qu'un endomorphisme g commute avec f il faut que f(g(u)) = g(f(u)).Soit donc un vecteur de base g(u). Son application par f donne l'image de f(u) par g. Ainsi, pour peu que u ne soit pas vecteur propre de f, l'application g est alors entièrement déterminé par la base (u, f(u)) et son image (g(u), f(g(u)).Ayant g déterminée par son image dans la base (u, f(u)), on peut ensuite utiliser l'une des macros de la page précédente pour construire l'image de v.On a ainsi construit une application g - pour laquelle g(u) est un vecteur de base - qui commute avec f. |
 |
|
|
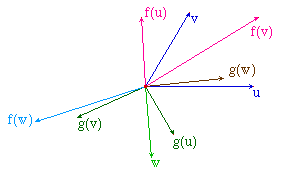
Considérons, sur la figure précédente, un nouveau vecteur w, et ses images f(w) et g(w).
|
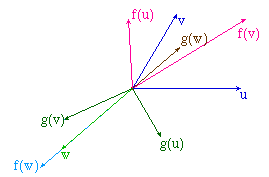
Cas d'une valeur propre positive pour f |
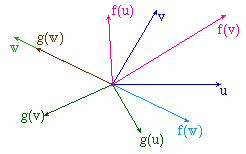
Cas d'une valeur propre négative pour f |
[Macros de base] [Trace] [Déterminant] [Illustration : endomorphisme de trace nulle]