Il s'agit simplement dans cette page d'illustrer comment une interprétation affine de certaines propriétés euclidiennes peuvent aboutir à des constructions affines dans des situations plus générales que celles construites autour de l'orthogonalité.

Plus précisément, il s'agit de voir comment résoudre certaines questions affines en sachant les traiter uniquement dans des cas particuliers euclidiens. Les illustrations proposées ici - trés classiques - vont porter sur la transformation de propriétés euclidiennes du cercle en des propriétés affines de l'ellipse.

Construction de l'ellipse de Steiner

Transformation en macro

Lecture affine des médiatrices d'un triangle inscrit dans un cercle

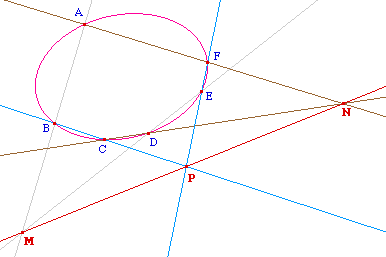
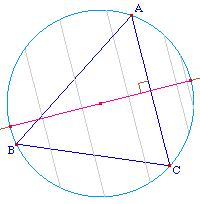
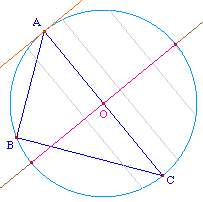
	Le segment de médiatrice d'une corde [AC] d'un cercle, interceptée par ce cercle est aussi le lieu des milieux des cordes parallèles à ce segment. Le milieu de ce segment lieu est le centre du cercle. On dispose donc là d'une lecture affine de la médiatrice d'une corde d'un cercle, et donc d'une construction, par des arguments affines du centre d'un cercle. ... par consséquent transposable sur une ellipse par transformation affine par conservation du parallèlisme.
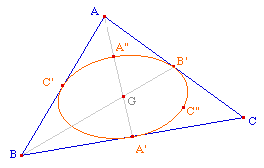
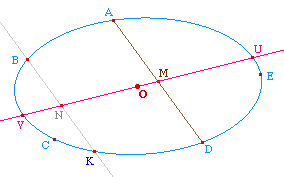
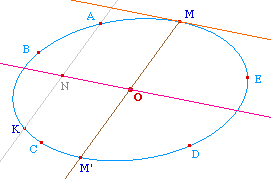
	Soit une ellipse définie par 5 points A, B, C, D, E. Notons M le milieu de le corde [AD] et N le milieu de la corde parallèle passant par B. La droite (MN) coupe l'ellipse en U et V. Le centre du cercle est le milieu de [UV]. Remarque 1 : Cette construction reste une construction "règle et compas" car on sait que l'intersection d'une droite et d'une conique est obtenue à la règle et au compas. Remarque 2 : La médiatrice d'une corde étant sa direction orthogonale, la direction des milieux de cordes parallèles est la direction conjuguée de celle des cordes.
	Cette seconde remarque permet la construction élémentaire de la tangente en un point de l'ellipse. En effet, une tangente en un point A d'un cercle est parallèle à la médiatrice du diamètre [AC], et donc parallèle au lieu des milieux des cordes parallèle au diamètre. Comme précédemment, puisque, cette fois, le contact est conservé par transformation affine, cette lecture de la construction convient pour une ellipse.
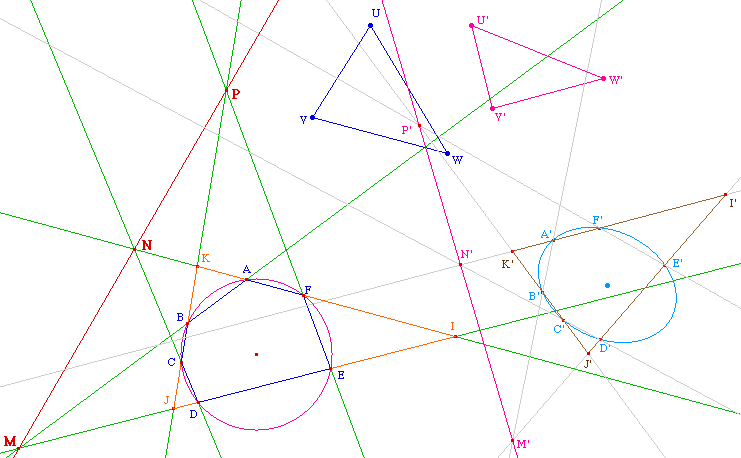
	Soit une ellipse, toujours définie par les 5 points A, B, C, D, E. Le centre O a été construit comme précédemment. Notons M un point de l'ellipse en lequel on souhaite construire la tangente. Soit M' le symétrique de M par rapport à O. et N le milieu de la corde paralléle à [MM'] passant par A. Alors, la parallèle à (ON) passant par M est la tangente à la conique en M. Remarque 3 : Cette construction permettrait aussi, pour l'ellipse, la construction du rayon conjugué à OM. TALAO3.fig

Compléments

Par des arguments projectifs de polaires, la construction du centre est encore correcte pour le centre d'une hyperbole, mais il faut opérer sur deux cordes car le lieu des milieux des cordes parallèles est cette fois une droite et elle peut ne pas couper l'hyperbole si les points A et C sont sur deux branches distinctes, on ne peut donc en prendre le milieu. De même, la construction de la tangente est elle aussi correcte puisque la direction construite est toujours la direction conjuguée.

Théorème de Pascal (version ellipse)

Le théorème de Pascal sur l'alignement des intersections des côtés opposés d'un hexagone quelconque inscrit dans un cercle (présenté à cette page) se transpose naturellement en une propriété de l'ellipse par transformation affine :

Ici la transformation affine qui envoie UVW sur U'V'W' envoie la configuration de gauche de l'hexagone inscrit dans un cercle sur son image dans l'ellipse image.

Bon, c'est clairement "un peu" grand, mieux vaut Lancer la figure TALAO4.fig pour y voir plus clair.

Mais on peut aussi le voir directement sur une ellipse :

 

Complément hors TAff

Lancer la figure TALAO5.fig histoire de voir ça de plus près.

Eh, oui, bien-sûr, c'est aussi vrai sur une hyperbole. Mais on quitte alors les TAff. Disons - en étant un peu rapide - que les TAff sont seulement parmi les transformations qui conservent l'alignement, celles, bien particulières, qui conservent aussi le parallélisme (c'est cette propriété qu'a étudié par exemple Möbius pour les définir).

Il y a donc des applications plus générales - les homologies - auxquels on peut appliquer ces questions d'incidence. Le lecteur curieux peut facilement transformer un cercle en hyperbole avec les arguments - et les figures à télécharger - présentés à la page homologie harmonique de la conférence de Michel Guillerault sur les coniques avec Cabri II. Il pourra alors faire la même figure que ci-dessus avec une homologie harmonique au lieu d'une transformation affine.

Cela dit, ceci est un point de vue sur les transformations. Le théorème de Pascal se montre trés simplement pour toute conique par des considérations barycentriques élémentaires.

Menu général