 TAOrtho1.fig
TAOrtho1.fig
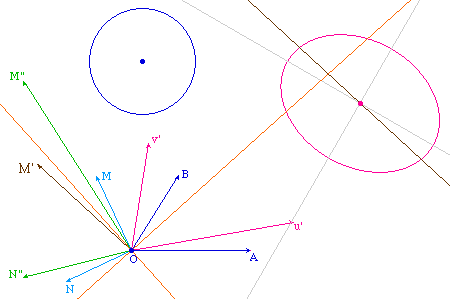
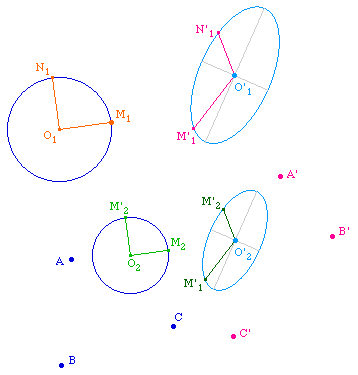
On sait que l'image, par une transformation affine (TAff), de deux droites orthogonales sont deux droites sécantes, en général non orthogonales. Ci dessous, dans la TAff qui envoie ABC sur A'B'C' on a construit l'ellipse de centre O'1, image d'un cercle de centre O1 et les images O'1M'1 et O'1N'1 de deux rayons orthogonaux O1M1 et O1N1 du cercle initial. Pour illustrer que la propriété est vectorielle, on applique la même construction à un second cercle, avec des rayons parallèles aux premiers. Les axes des deux coniques sont tracés par une macro indépendante ( AxesHE.mac de la page Axes par point de Fregier )
On observe tou d'abord que les axes des deux ellipses sont parallèles (respectivement) et donc que leurs directions est une propriété vectorielle liée à la TAff. On peut par exemple déplacer le centre O2 du second cercle pour observer que les directions des axes restent les mêmes.
Or la donnée d'un cercle et d'une conique est aussi celle d'une forme quadratique - dont la conique peut être considérée comme la ligne de niveau q(x) = 1 - dans un espace vectoriel muni d'un produit scalaire - dont le cercle est la ligne de niveau 1. Le théorème de diagonalisation simultanée dit justement qu'il existe une base orthonormale pour le produit scalaire qui est orthogonale pour la forme quadratique, c'est-à-dire ici, puisque nous somme dans le plan affine, qu'il existe deux rayons orthogonaux d'origine O1 qui auront pour image deux rayons conjugués portés par les axes, comme on peut l'observer ci-dessous :
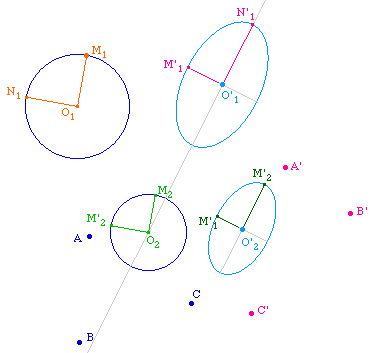
Autrement dit, nous venons d'illustrer, pour le plan affine, le résultat suivant :
Pour toute application affine d'un espace euclidien, il existe une base orthonormale dont l'image est une famille orthogonale.
Ici comme nous sommes en dimension 2 et que l'on s'intéresse aux bijections affines, on peut traduire plus simplement en :
Pour toute transformation affine du plan, il existe un couple de directions orthogonales qui ont pour images deux directions orthogonales.