On se propose ici seulement d'illustrer les premières propriétés des transformations affines en invitant à les tester sur quelques figures Cabri.

Conservation du parallèlisme

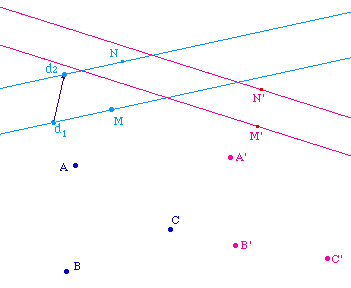
L'image, par une transformation affine (TAff), de deux droites parallèles sont deux droites parallèles.   Dans l'illustration ci-contre, M décrit une droite, N une droite parallèle, leurs images M' et N' décrivent deux droites parallèles. Différents types d'expérimentations seraient envisageables en TP ici ... TADrPara.fig

Conservation du contact

L'image, par une TA, de deux courbes tangentes en un point sont deux courbes tangentes en le point image. Nous proposons trois illustrations :

Cercle et droite

 

TACntDC.fig En déplaçant le point M l'image de la tangente décrit l'ensemble des tangentes à la conique. On pourrait aussi faire l'enveloppe de tangentes, ou encore vérifier expérimentalement que la droite image coïncide avec la tangente à la conique en M'.

Cercle et cercle

TACntCC.fig

Le premier cercle est de base. Sur ce cercle on peut déplacer M et sur la droite (O₁M) modifier le rayon du second cercle.

Conique et cercle osculateur

TAOscul1.fig

La conique est modifiable par ses 5 points constituants. Le point M est sur objet sur la conique, le cercle est le cercle osculateur en M : son contact est de degré 3 avec la conique, il ne coupe la conique qu'en un seul autre point : il en est donc de même avec les deux coniques images, qui ont ainsi un contact d'ordre 3.

Menu général