[Macros
de base] [Parallélisme
et contact] [Taff
et orthogonalité]
[Lecture affine de
l'orthogonalité]
[Retour 2D
Géné]
|
|
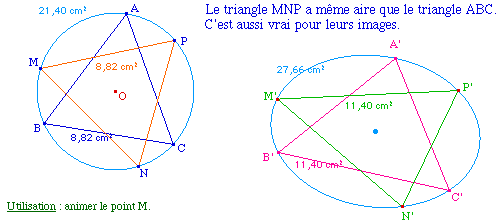
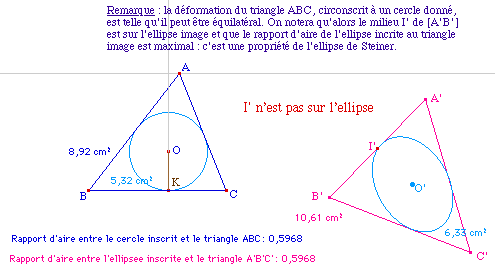
Les coordonnées barycentriques étant conservées par une application affine, et l'image d'un repère affine étant un repère affine pour une transformation, la notion de rapport d'aire peut être considérée comme une propriété (des transformations) affine(s). |

|
|
Pour qu'une transformation affine plane conserve les aires, il faut que son application vectorielle associée soit de déterminant 1 ou -1, c'est-à-dire que l'application affine transforme un triangle en un triangle de même aire. Commençons donc par construire un triangle A'B'C' de même aire que ABC : A' et B' seront deux points de base, et C' sera un point lié à une droite :Sur la demi-droite [A'B') on reporte A'B1 : la mesure c de [AB]. Sur la perpendiculaire en A à [A'B'], on reporte la longueur h le la hauteur de ABC issue de C. Une simple application de Thalès permet de construit le produit c.h, sur la perpendiculaire, dans l'unité A'B'. Le point C' est donc sur la parallèle à (A'B') passant par ce point ch. |
|
|
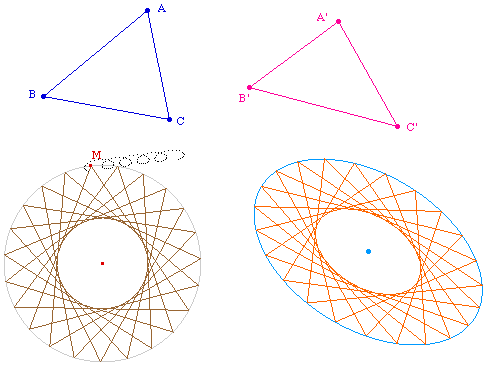
Une transformation affine étant définie par {A, B, C} et son image dans {A', B', C'}- ci dessous avec les correspondances des lettres - on peut comparer les aires d'un polygone et de son image, d'un cercle ou d'une ellipse et de son image :
|
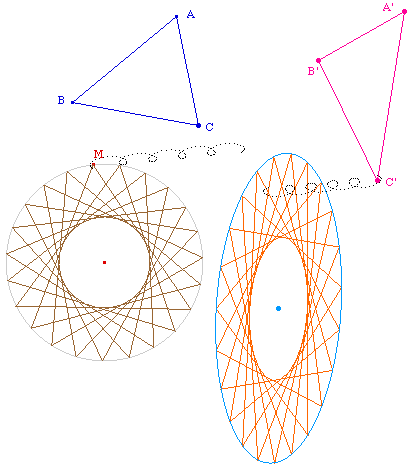
[Macros
de base] [Parallélisme
et contact] [Taff
et orthogonalité]
[Lecture affine de
l'orthogonalité]
[Retour 2D
Géné]