Théorème de Morley

4 - Autres triangles équilatéraux de la configuration
4D - Neuf autres triangles aux côtés parallèles 3 à 3

 

 [Partie 4A] [Partie 4B] [Partie 4C]

   [1 - Théorème initial] [2 - Les 6 trissectrices d'un angle - Notations] [3 - Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles équilatéraux de la configuration ] [5 - Commentaires et figures finales] [6 - Compléments]
[7 - Historique et Références] [Retour "Grands Classiques"] [Retour "Géométrie Plane"]

 

Les 9 triangles restant - sauf une autre partition à trouver - ne semblent pas avoir de relation élémentaires avec les trissectrices comme les précdents. Il reste qu'ils ont cette particularité de pouvoir être classés en trois groupes de trois triangles ayant leurs côtés parallèles entre eux.

 

Rappel : tous les résultats et classements proposés dans ces pages 4A à 4D sont simplement des résultats expérimentaux obtenus par l'utilisation de Cabri.

 

Premier groupe de trois triangles aux côtés parallèles

 

 

Détail des triangles

 

Les côtés d'une même ligne du tableau sont parallèles entre eux

Triangle 1

Triangle 2

Triangle 3

B2C3 - B4C5

B6C5 - B2C1

B4C1 - B6C3

B4C5 - B6C1

B2C1 - B4C3

B6C3 - B2C5

B6C1 - B2C3

B4C3 - B6C5

B2C5 - B4C1

MRL9a.fig (intermédiaire dans cette position)

 

Deuxième groupe de trois triangles aux côtés parallèles  

 

 

 

 

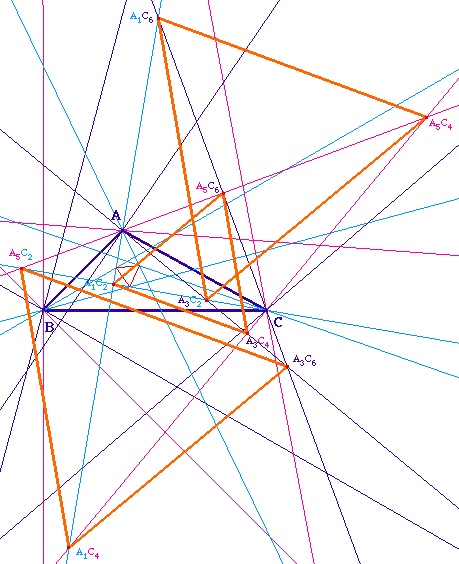
Les côtés d'une même ligne du tableau sont parallèles entre eux

Triangle 1

Triangle 2

Triangle 3

A1C4 - A3C6

A3C2 - A5C4

A5C6 - A1C2

A3C6 - A5C2

A5C4 - A1C6

A1C2 - A3C4

A5C2 - A1C4

A1C6 - A3C2

A3C4 - A5C6

MRL9b.fig (intermédiaire dans cette position)

 

Troisième groupe de trois triangles aux côtés parallèles  

 

 

 

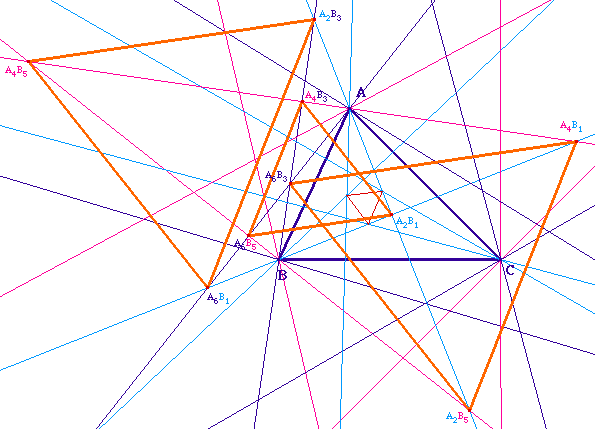
Les côtés d'une même ligne du tableau sont parallèles entre eux

Triangle 1

Triangle 2

Triangle 3

A2B1 - A4B3

A4B5 - A6B1

A6B3 - A2B5

A4B3 - A6B5

A6B1 - A2B3

A2B5 - A4B1

A6B5 - A2B1

A2B3 - A4B5

A4B1 - A6B3

MRL9c.fig (intermédiaire dans cette position)

 

Les 9 triangles ensemble

 

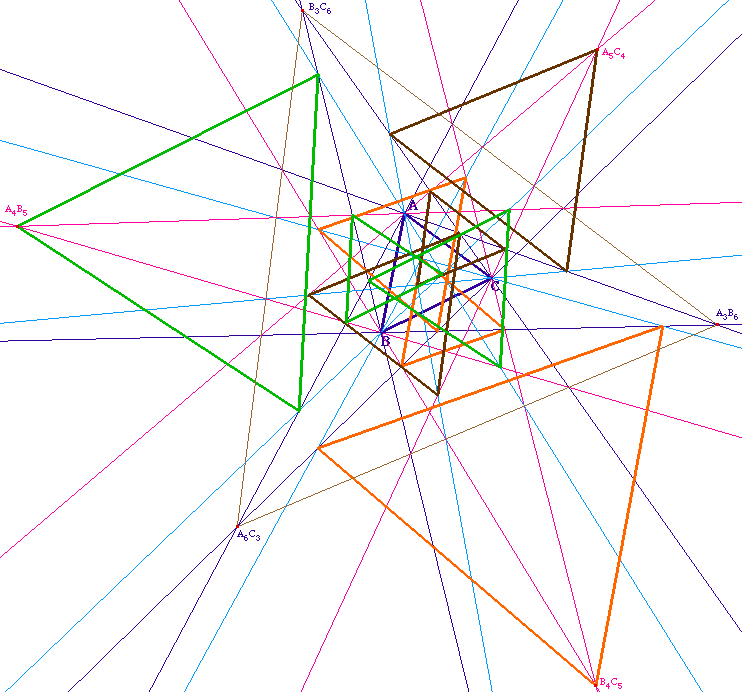
  MLR9abc.fig (intermédiaire dans cette position)

On a placé le triangle extérieur de la configuration de Morley (A3B6 - B3C6 - A6C3). On remarquera que le triangle A4B5 - B4C5 - A5C4 n'est pas équilatéral.

Il ne semble pas qu'une autre partition permette de déceler plus de régularité sur ces 9 triangles. En chargeant la figure, on pourra toutefois s'y essayer. On remarquera par ailleurs - en la transformant en macro - la situation particulière obtenue quand le triangle de départ est équilatéral ...

 

 [Partie 4A] [Partie 4B] [Partie 4C]

   [1 - Théorème initial] [2 - Les 6 trissectrices d'un angle - Notations] [3 - Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles équilatéraux de la configuration ] [5 - Commentaires et figures finales] [6 - Compléments]
[7 - Historique et Références] [Retour "Grands Classiques"] [Retour "Géométrie Plane"]

 

 

Menu général