
4 - Autres triangles
équilatéraux de la
configuration
4B - Cotés parallèles aux trissectrices issues de
B

(par côtés) |
(par côtés) |
(par côtés) |
la trissectrice |
|
|
|
|
|
|
|
|
|
|
|
|
![]() MRLb135.fig (intermédiaire
dans cette position)
MRLb135.fig (intermédiaire
dans cette position)
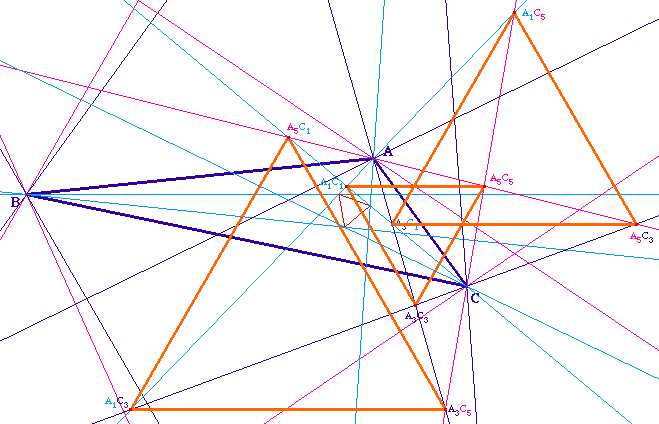
(par côtés) |
(par côtés) |
(par côtés) |
la trissectrice |
|
|
|
|
|
|
|
|
|
|
|
|
![]() MRLb246.fig (intermédiaire
dans cette position)
MRLb246.fig (intermédiaire
dans cette position)
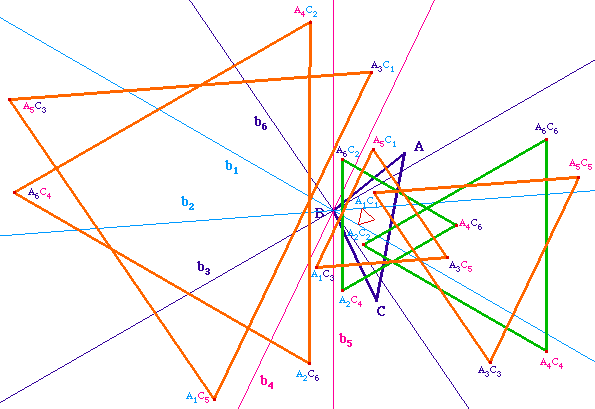
![]() MRLbb.fig (intermédiaire
dans cette position)
MRLbb.fig (intermédiaire
dans cette position)