IV.2.b - Constructions d'angles particuliers

[IV.2.a. Marque et mesure d'angle] [IV.2.c. Trigo hyperboliques] [IV.2.d. Triangles et isométries]

D'une manière générale, on a vu à la page précédente que les macros de report d'angle sont assez lourdes. Pour certains type d'exercice, on peut avoir besoin d'angles particuliers. Nous nous proposons de réaliser quelques macros autour de ce thème. Ce sera aussi l'occasion d'approfondir un peu plus notre pratique de l'orientation avec Cabri et de construire quelques lieux sympathiques.

Angle orienté de 45 degrés

a - Principe du report de 45 degré orienté - problème d'orientation

Pour le report d'un angle donné, nous avions utilisé la composée de deux symétries orthogonales euclidiennes. L'angle n'étant pas donné, il faut opérer autrement. Pour un angle de 45 degrés, on peut penser à des constructions élémentaires avec perpendiculaire, cercle et milieu hyperboliques. Bien-sûr, mais comme ces items utilisent chacuns plusieurs objets euclidiens, on arrive à la construction d'un angle de 45 degrés en plus de 80 objets intermédiaires, et c'est justement ce que l'on souhaite éviter.

L'idée est de reprendre la construction de base pour la mesure d'un angle, en prenant à priori une droite à 45 degrés de la tangente. Pour cela, on projette B sur la tangente, ce qui donne le point U. Le cercle de centre A passant par U coupe la normale (AIAB) en V. On prend - au choix - la bissectrice de UAV ou la médiatrice de [UV]. Dans un cas de courbure (illustration de gauche, en rose) on a bien une droite à + 45 degrés, mais quand la courbure du segment hyperbolique change, la droite est à - 45 degrés de la tangente (illustration de droite). HAngl09a.fig

Le point V est toujours celui que l'on a pris au départ, le problème vient de ce que ce point V sur le cercle doit-être, selon la courbure du segment hyperbolique - rappelons que l'on passe d'un arc de cercle à un autre arc de cercle pour le dessin Cabri - celui choisi (ie de l'autre côté du centre par rapport à la tangente (AU) ou l'autre, du même côté que le centre par rapport à la tangente, ce qui se voit bien sur la seconde illsutration. Il convient de rendre compte de ceci avec Cabri.

abraCAdaBRI est intéressé par quelques informations supplémentaires sur les raisons de cette solution ...d'un lecteur curieux - où une personne impliquée dans le développement de Cabri - qui fouillerait cette construction plus à fond.

b - La construction effective

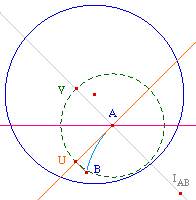
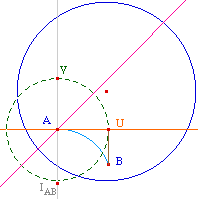
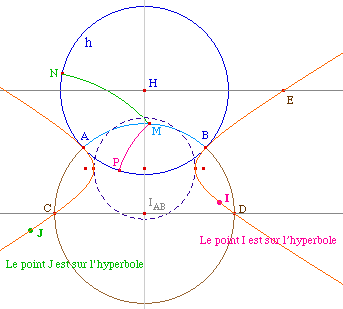
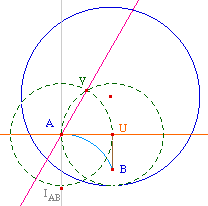
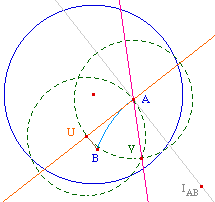
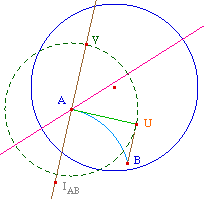
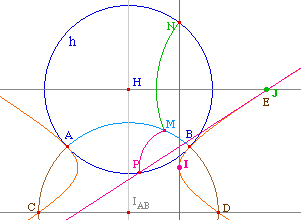
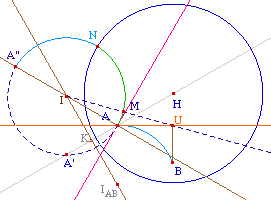
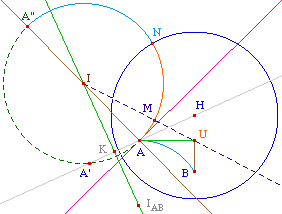
On reconstruit la droite des centres des droites hyperboliques passant par A par la perpendiculaire à (HA') en K milieu de [AA'] (avec A' inverse de A). Le centre I de la demi-droite hyperbolique cherchée est l'intersection de cette droite et de la perpendiculaire à la droite à 45 degrés (rose). Le cercle de centre I passant par A recoupe (IA) en A". Par précaution, on construit la solution en deux étapes : comme l'unique intersection d'un arc avec l'horizon. Cet arc sera AA" pris dans le bon sens, c'est-à-dire passant par un point qui est trivialement sur le bon arc : ici on a choisi M intersction du cercle avec la demi-droite [IU). 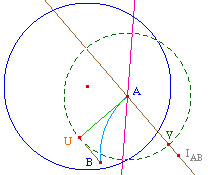La solution est alors l'arc AMN où N est l'intersection de l'arc précédent avec l'horizon. HAngl09c.fig ou APlus45.mac (Objets initiaux A, B, IAB, l'horizon, 21 objets intermédiaires ... tout de même)

En redéfinissant le point V comme étant l'autre intersection on a aussitôt la figure qui donne un arc de - 45 degrés :

HAngl09d.fig ou AMoins45.mac

 

c - illustration : approche expérimentale sur une hyperbole

On a vu à la page précédente que la connaissance de deux angles d'un triangle ne détermine pas le troisième. Donc si on veut construire des triangles d'angles donnés, il va être nécessaire de construire des segments de longueur précises. Pour cela, on peut choisir de recourir au calcul, comme on le fera à la page suivante, avec le calcul trigonométrique hyperbolique, mais il est intéressant de chercher des solutions géométriques. Ainsi, est-on amené à s'intéresser au lieu des centres des demi-droites d'angle donné avec une droite donnée pour construire ensuite un arc de cercle dont le centre sera obtenu comme intersection de deux tels lieux. Cette approche préliminaire est l'objet de ce paragraphe, dans le cas bien particulier de l'angle construit ci-dessus.

 

A et B sont deux points idéaux d'une droite hyperbolique. On considère un point M de cette droite, et on s'intéresse aux centres I et J des demi-droites d'origine M qui font un angle de + 45 et - 45 degrés avec l'arc AM. Le fait d'avoir pris des points idéaux pour définir la droite évite les questions d'inversion d'orientation. Ci-contre, les lieux de I et J. On pense naturellement, pour la réunion des deux lieux, à une hyperbole, nécessairement tangente à l'horizon en A et B, ceux deux points étant exclus du lieu. En prenant 5 points sur objets du lieu, on peut confirmer cette hypothèse avec la vérification d'appartenance de Cabri. Toutefois l'appartenance n'est pas tout à fait stable. Il est intéressant de prendre 5 points bien particuliers de cette hyperbole. HAngl10a.fig

Remarque : on notera N et P les points idéaux des demi droites construites. On peut dire alors que MNP est un triangle rectangle en M dont la somme des angles fait 90 degrés. On s'intéresse alors au lieu des centres des côtés de l'angle droit quand M décrit une bissectrice fixée par avance.

On observe par exemple que les points C et D, intersection du cercle support de la droite hyperbolique et de la perpendicualaire à la droite des deux centres en IAB sont deux points de l'hyperbole (cas où M est au milieu - euclidien - de l'arc AB. On a donc 4 points de l'hyperbole et deux tangentes, on pourrait ainsi construire l'hyperbole. Le choix illustré à gauche a plutôt été de construire un cinquième point, le point E de l'hyperbole sur la perpendiculaire en H à la droite des centres (HIAB) : E est construit comme centre d'un cercle orthogonal à l'horizon et faisant un angle de 45 degrés avec le cercle support de (AB).En construisant cette hyperbole par 5 points, l'appartenance de I et J à l'hyperbole est confirmée sauf pour quelques positions bien particulières (arcs passant par H, les centres sont alors à l'infini dans la direction d'une asymptote). On notera également que P est l'inverse de N dans l'inversion d'arc (AB). HAngl10b.fig où on été ajoutés comme ci-contre les sommets, le cercle principal et les foyers qui se déduisent facilement de la construction de E ... en utilisant les remarques suivantes :

En effet, cette hyperbole (qui existe pour tout angle non nul et non plat) a, pour ce cas de 45 degrés, cette propriété particulière que la tangente à la conique en J - centre de l'arc idéal MN - est la droite (JP) où P est le point idéal de l'autre arc. De même la tangente en I est la droite (IN) comme illustré ci-dessous à gauche.

Enfin, mentionnons que l'on construit facilement un sommet en observant que quand J est au point E construit préalablement - il a été choisi pour cela - alors I est au sommet de l'hyperbole sur la même branche (illustration de droite). Le sommet est obtenu - toujours expérimentalement dans un premier temps ! - comme l'intersection de la droite des centres (EI_AB) avec l'axe radical de l'horizon et du cercle qui lui est orthogonal de centre E, support de l'arc MN.

Tout ceci, et une généralisation à un angle quelconque sera l'occasion de rédiger un joli exercice sur le thème des angles. Dans ce cas particulier, les preuves et les constructions sont élémentaires, dans le cas général, les constructions sont nécessairement un peu plus longues, et, si le fait que N et P soient inverse l'un de l'autre dans l'inversion de la droite (AB) est toujours vrai, la propriété des tangentes reste propre à cet angle particulier. On verra alors pourquoi.

Angle orienté de 60 degrés

a - la construction

Pour un angle de 60 degré, la construction par intersection des cercles centrés en A et U est indépendante de l'orientation des droites, la droite (AV) fait donc bien un angle de + 60 degrés par rapport à (AU) quelque soit la courbure de l'arc AB. HAngl11a.fig

La construction se fait alors exactement comme ci-dessus :   HAngl11b.fig ou APlus60.mac De même, en redéfinissant V comme étant l'autre intersection des deux cercles de centre A et U, on obtient une figure prête pour réaliser une macro d'angle de mesure "négative" : HAngl11c.fig ou AMoins60.mac

b - le lieu des centres des demi-droites d'angle géométrique 60 degrés par rapport à une droite

HAngl12a.fig

 

Avec les mêmes objectifs et les mêmes notations que ci-dessus, on observe expérimentalement quelques points de l'hyperbole lieu des points I et J : le cercle de centre H - centre de l'horizon - passant par le centre I_AB de la droite hyperbolique coupe cette droite en deux points C et D que l'on conjecture sur l'hyperbole. De même en considérant le centre de centre V passant par U, on trouve E et F. Nous avons donc 5 points pour construire la conique, et on Cabri-vérifie que I et J appartiennent bien à l'hyperbole passant par ces 5 points.

HAngl12b.fig (l'hyperbole construite et les vérifications)

Ces deux hyperboles permettront, ultérieurement, de construire de manière purement géométrique un triangle isocèle ayant un angle au sommet de 60 degrés et deux angles égaux à 45 degrés. Ce triangle permettant lui-même de construire aisément un hexagone régulier ayant six angles droits.

 [IV.2.a. Marque et mesure d'angle] [IV.2.c. Trigo hyperboliques] [IV.2.d. Triangles et isométries]

Menu général