 Dans le plan projectif, considérons une conique non dégénérée, appelée absolu. On peut alors définir les distances par :
|
|
![]()
[Synthèses] [Riemann] [Hilbert]
[Présentation chronologique] [Précurseurs] [Fondateurs][Lobachevsky]
[Retour aux GNE] [Références utilisées] [Menu général]
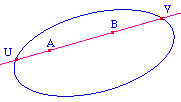
 Dans le plan projectif, considérons une conique non dégénérée, appelée absolu. On peut alors définir les distances par :
|
|
![]()
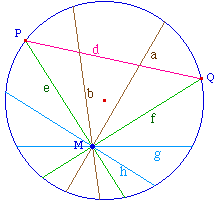 |
Un plan hyperbolique est un plan dans le quel il existe au moins deux droites non connectables (ie sans point commun et sans perpendiculaires communes) et tel que pour tout point A n'appartenant pas à une droite d, il existe au moins une droite passant par A non connectable à d.Ci-contre, la distance de A et B est d(A,B) = |ln[(AU/AV)/(BU/BV)]|Parmi les droites du faisceau issu de M, on distingue
|
|
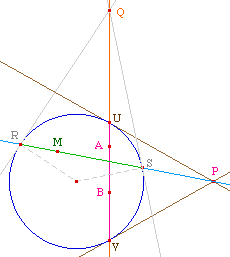
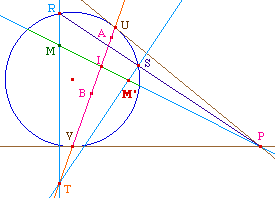
L'orthogonalité est bien une relation symétrique |
|
|
|
 |
|
Depuis la rédaction de cette page, un dossier assez consèquent sur le modèle de Klein - Beltrami a été mis en ligne ici.
[Présentation chronologique] [Précurseurs] [Fondateurs] [Lobachevsky]