|
|
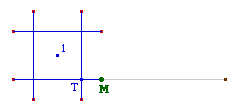
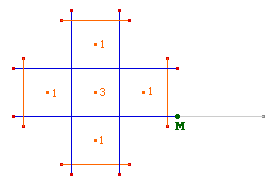
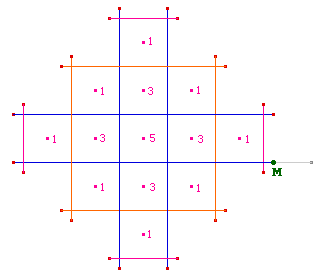
Cette figure Cabri va vous permettre de simuler la
croissance du Réseau dans un de ses plans de
symétrie, l'intérêt principal
étant de voir les générations de cubes
se former et d'aider les élèves à
compter les cubes superposés au centre de chaque
carré. Vous imaginez donc que, à une
génération donnée, vous applatissez le
réseau entier sur un plan de symétrie du
réseau. Nous allons simuler cette projection
jusqu'à la troisième
génération.
Voir plutôt une
animation
gif de la
figure 2D
(36 Ko)
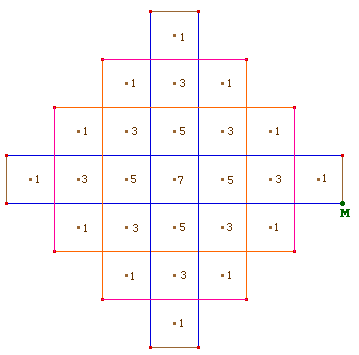
Ci-contre :
Illustration de la projection
à la génération 3
|