1.a Trissection de l'angle
Pierre Delezoïde - Lycée Buffon - Paris XV°
[Retour Conique] [Autre utilisation des coniques] [Menu Général]
1. La construction proposée par l'auteur (agrémentée "d'abraCAdaBRI remarques" sur l'art de l'intersection dans Cabri)
2. L'écriture (mathématiquement approximative) de cette preuve en ligne, pour une approche des idées générales.
Pour une impression de qualité, on choisira l'article original de Pierre Delezoïde, déchargeable au format Postscript Hepta.ps (104 Ko) ou au format PDF Hepta.pdf (80 Ko), ou au format TeX (en cours).
Pour le .pdf, penser à faire "enregistrer sur disque" si vous ne voulez pas lancer le plug in ....
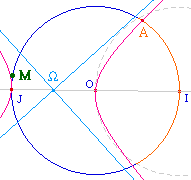
Construction : On considère un point M, d'affixe u de module 1, donc sur le cercle de centre O de rayon 1 (point I). Soit J le point d'abscisse -1 (avec Cabri, prendre l'intersection du cercle et de la droite (OI) : le point J sera connu par Cabri comme étant un point du cercle.
|
|
On considère d la bissectrice intérieure de l'angle IOM. Soit W (oméga sur l'illustration) le milieu de [OJ]. Alors l'hyperbole équilatère de centre W passant par O et dont une asymptote est parallèle à la bissectrice des droites d et (OI) coupe le cercle trigonométrique en J et en trois autres points, sommet d'un triangle équilatéral - qui sont les racines cubiques de u.On confirme (ci-contre) la trissection de l'angle IOM ... et au passage la remarquable précision de Cabri ! |
|
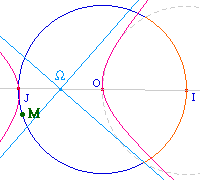
Questions de stabilité : on sait que, dans la version actuelle de Cabri (09/98) l'ordre des intersections avec les coniques ne sont pas stable par manipulation directe. Cette construction reste correcte pour tout M restant avec un argument de 0 à Pi. Sinon, le triangle passe par le point J. Il est possible que la version Windows, plus récente, soit plus stable sur ce point.
Toutefois, on peut raisonnablement espérer que la séparation des racines soit facilement accessible ici par l'intersection de l'hyperbole équilatère et d'un arc de cercle, en effet, comme le fait remarquer Pierre Delezoïde dans son article, on s'intéresse alors à la racine comprise entre -Pi/3 et Pi/3. Hélas, il semble bien que ce soit un leurre graphique car le point d'intersection construit n'est pas le même quand M décrit le cercle : entrons une nouvelle fois en détail dans les subtilités de l'intersection avec Cabri, avec la version actuelle (1.1.5 au 09/98).
Intersection de deux objets / intersection en manipulation directe
|
|
|
|
On utilise le curseur, et on montre "point à
cette intersection". La construction est
réputée plus stable, justement, en particulier
avec les arcs de cercle (voir aussi cette
page hyperbolique). Mais attention, si on lève
une ambiguïté, on revient dans le mode
d'intersection de deux objets - puisque l'on montre les deux
objets. Par exemple ici, il faut
cacher le cercle ce centre O, avant de prendre
l'intersection avec le curseur en s'approchant du
point voulu.
On voit à droite que le
point A n'existe plus quand M a dépassé J
...
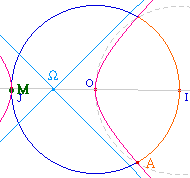
Pourtant, quand M est en J, A passe bien de l'autre
côté ....
pourquoi n'y reste-t-il pas ?abraCAdaBRI est intéressé par tout autre
type d'expérimentation ayant pour but de mieux
stabiliser ce type d'intersection puisque, pour l'instant,
la macro Trissection ne fonctionne correctement que sur la
partie des points d'affixe x + i y avec y > 0.
![]() Trissect.mac (objets
initiaux O, I, M obtjet final le point A)
Trissect.mac (objets
initiaux O, I, M obtjet final le point A)

En choisissant l'une des méthodes d'intersection
pour obtenir le point A, la racine cubique entre -Pi/3 et
Pi/3, on peut construire alors à la règle et
au compas les deux autres, puisqu'il suffit de faire une
rotation de 2Pi/3.
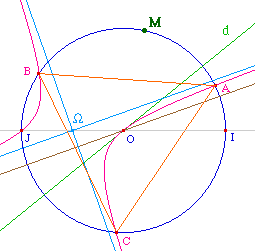
Ci-contre on a choisit une méthode "longue" : il
aurait été plus facile de prendre le cercle de
centre le symétrique de A par rapport à O et
passant par O. Et même avec la construction de cercles
intermédiaires, Cabri confirme que les points U et V,
construit comme intersection de cercles, sont bien sur
l'hyperbole équilatère.
(1)
avec a et b complexes, r et s réels, et (a, r) différent de (0, 0).
(S)
 |
Une manière simple et symétrique par rapport à la variation de u est de choisir, parmi toutes les hyperboles équilatères possibles celle dont le quatrième point d'intersection avec le cercle est le point d'affixe -1. Le centre de l'hyperbole est alors le point d'affixe -1/2. On vérifie que si la droite d est la bissectrice intérieure de l'angle IOM, les asymptotes de l'hyperbole sont alors les bissectrices des droites (OI) et d, ce qui permet sa construction.
Note : ici la droite d est la tangnete à l'hyperbole en O, ce qui donnerait une autre approche possible pour la construction de l'hyperbole. |