1.b Construction de l'heptagone régulier
Pierre Delezoïde - Lycée Buffon - Paris XV°
[Retour Conique] [Autre utilisation des coniques] [Menu Général]
1. La construction réalisée par l'auteur
2. L'écriture (mathématiquement approximative) de cette preuve en ligne, pour une approche des idées générales.
Pour une impression de qualité, on choisira l'article original de Pierre Delezoïde, déchargeable au format Postscript Hepta.ps (104 Ko) ou au format PDF Hepta.pdf (80 Ko), ou au format TeX (en cours).
Pour le .pdf, penser à faire "enregistrer sur disque" si vous ne voulez pas lancer le plug in ....3. Extraits d'un sujet de CAPES interne relatif à cette construction
|
|
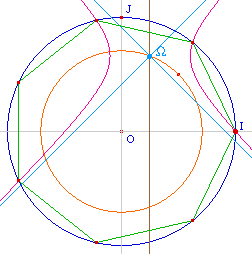
On se propose de construire une hyperbole équilatère coupant le cercle trigonométrique au point I d'affixe 1 et en trois autres points appartenant à l'heptagone régulier ayant I pour sommet, les trois derniers points de l'hepagone étant les conjugués de ceux ci. Les détails des calculs aboutissant à cette construction sont proposés ci-aprés.Etant donné un cercle de centre O passant par I - cercle unité - on construit l'intersection (une des deux) de la droite d'équation x=1/4 avec le cercle de centre O et de rayon Rac(2)/2 : ce cercle passe par le milieu de [IJ] (ci-contre). Soit W (lire oméga) ce point.On trace, par la macro rappelée ci-dessus, l'hyperbole équilatère de centre ce point W, passant par I et admetant pour direction asymptotique les bissectrices des axes.Cette hyperbole coupe le cercle en trois points de l'heptagone que l'on termine en prenant les conjugués. |
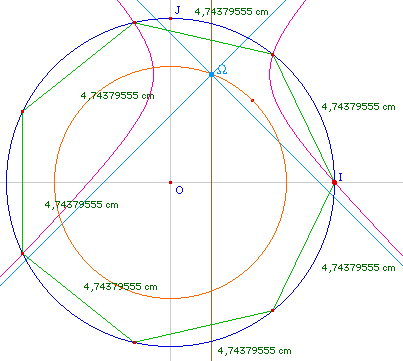
Vérification sur les longueurs : on a
une précision à 10-8 cm !!!
![]() HeptaD02.fig
HeptaD02.fig