3 - Lieu du 2° foyer d'une conique connaissant un foyer, une tangente et un point
[1
- Cercle circonscrit et cercle
d'Euler]
[2
- Conique définie par cercle principal et deux tangentes
]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exercices
sur l'approche "bifocale"]
|
|
Proposons nous de construire un second foyer F' comme centre du cercle directeur associé au foyer F pour une conique de foyer F passant par A et admettant T pour tangente :On peut construire une tangente à la conique en A. Pour cela, on peut partir d'un point I du cercle de diamètre [AF]. Dire que (IA) est tangente en A à la conique revient à dire que le symétrique M de F par rapport à (IA) appartient au cercle directeur associé à F, donc que le second foyer F' de la conique est sur la droite (AM).Par ailleurs, puisque T est aussi une tangente, le symétrique N de F par rapport à la droite T appartient alors à ce même cercle directeur , et son centre F' est aussi sur la médiatrice de [MN].On construit ainsi F' et la conique par l'une des deux macros ci-dessus.
|
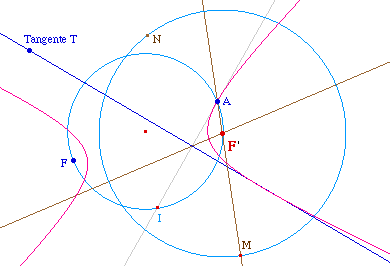
Cas où la conique est une hyperbole
|
|
Pour expérimenter sur le lieu de F', il suffit de faire son lieu quand I décrit le cercle de diamètre [AF] :
On obtient une conique, qui est manifestement elle aussi tangente à la droite T et qui semble avoir les points A et N comme foyers. |
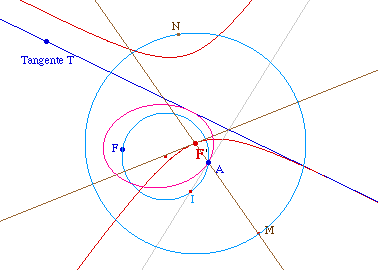
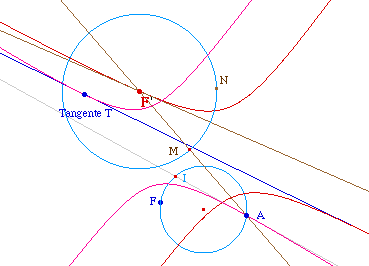
Renforcement des
conjectures : pour étudier le lieu, on peut
construire, par la macro d'introduction, la conique de foyers A et N
et de tangente T. On constatera qu'elle recouvre bien le lieu. On
remarquera aussi que le cercle de centre le milieu de [AN] et
de diamètre [AF] est manifestement le cercle principal
du lieu-conique.
Avant d'aborder une preuve des conjectures, il est trés intéressant d'étudier la nature de la conique de foyers F et F'. Disponible également dans une autre page pour avoir les deux à l'écran. En résumé, on montre (trés simplement) que :
Si A et F sont d'un même côté de la tangente T, la conique est soit une ellipse, soit une hyperbole, et dans ce cas M est toujours entre A et F'.
Si A et F sont de part et d'autre de la tangente, la conique est toujours une hyperbole, et c'est alors F' qui est toujours entre M et A.
|
|
Si F et A sont de part et d'autre de la tangente TOn a vu que F' est entre M et A. On a alors :AM = AF, une constante de la figure
|
|
|
Si F et A sont d'un même côté de la tangente TOn a toujours les deux égalités :AM = AF, une constante de la figure
|
|
|
Si la conique est une hyperbole, on a vu que M est toujours entre A et F', soit :
|