En cherchant à construire les coniques dont on connaît son premier foyer F, une tangente T et un point A, nous nous sommes aperçu qu'elle peuvent être de nature différente. Observons cela en détail.

Expérimentation

Si cela n'a déjà été fait, on peut

La figure ExLieu01.fig précédente

On observera que si F et A sont de part et d'autre de la tangente, la conique est toujours une hyperbole , alors que s'ils sont d'un même côté, selon la position de I sur le cercle de diamètre [AF] la conique est soit une ellipse soit une hyperbole - et serait une parabole à la frontière entre les deux si on ne cherchait pas des coniques bifocales, le point F' étant renvoyé à l'inifin dans ce cas. On se propose de déterminer cette frontière.

Distinction entre ellipse et hyperbole

La conique de foyers F et F' passant par A est une ellipse si et seulement si A est entre M et F' puisque F' est le centre du cercle directeur associé à F. Notons que quand I décrit le cercle de diamètre [AF], M décrit le cercle de centre A passant par F, et donc AM = AF. Alors, sur la droite (MA), A est entre M et F' si et seulement si la médiatrice de [MN] coupe la demi-droite [MA), mais ne coupe pas le segment [MA].

Si F et A sont de part et d'autre de la tangente T, A et N (symétrique de F par rapport à T) sont d'un même côté de T, médiatrice de [FN]. On a donc AF > AN, soit AM > AN. Ainsi, A et N sont du même côté de la médiatrice de [MN], donc le segment [AM] coupe la médiatrice de [MN], ainsi, F' est toujours entre A et M, la conique est toujours une hyperbole, quelque soit la position de M.

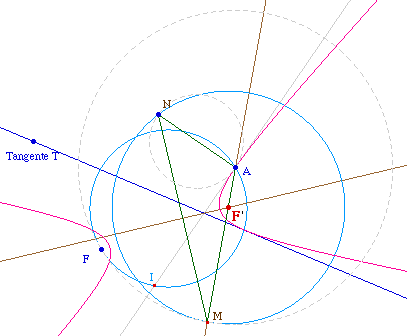
Cas où la conique est toujours une hyperbole

 

Si F et A sont d'un même côté de la tangente T, remarquons que la médiatrice de [MN] ne coupe jamais le segment [MA]. En effet, comme dans le cas précédent, il est immédiat que dans ce cas, AN > AM donc que c'est le segment [AN] qui rencontre la médiatrice de [MN]. On exclu en effet ici le cas du triangle isocèle (AM = AN) car alors le point A de la conique serait aussi son foyer ce qui est impossible.

Ainsi, dans ce cas, de la double condition mentionnée ci-dessus, l'une est toujours vérifiée, il reste donc que la conique est une ellipse si et seulement si la médiatrice de [MN] coupe la demi-droite [MA). Cette condition se traduit immédiatement en terme d'angle géométrique : la conique est une ellipse si et seulement si l'angle en M du triangle AMN est aigu, soit encore M est extérieur au cercle de diamètre [AN].

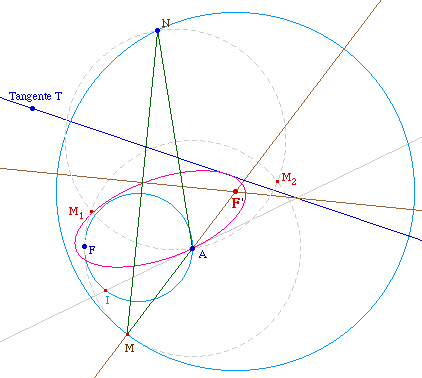
Cas où la conique est une ellipse

 

Or dans ce cas où F et A sont du même côté de la tangente T - médiatrice de [FN], le cercle de centre A passant par F coupe toujours le cercle de diamètre [AN] (alors que dans le cas précédent, l'un est contenu dans l'autre). Il y a donc deux points M₁ et M₂ sur le cercle de centre A passant par F pour lesquels F' n'existe pas car, le triangle AMN étant alors rectangle, (AM) et la médiatrice de [MN] sont parallèles. Sur l'un des arcs d'extrémité M₁ et M₂, la conique est une ellipse, sur l'autre une hyperbole.

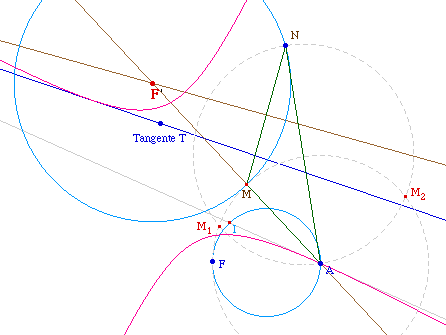
Cas où la conique est une hyperbole

La figure ExLieu02.fig ci-dessus

Remarque : Pour M en M₁ ou M₂, la parabole de directrice (MN) et de foyer F passe par A et est bien tangente à T, le second foyer F' est renvoyé à l'infini. On peut compléter la figure précédente en

Chargeant la macro Parabole par foyer directrice (fichier Parabole.mac)

En résumé ... pour la suite

Si A et F sont d'un même côté de la tangente T, la conique est soit une ellipse, soit une hyperbole, et dans ce cas M est entre A et F', car F' appartient à la droite (MA) mais pas à la demi-droite [MA).
Si A et F sont de part et d'autre de la tangente, la conique est toujours une hyperbole, et c'est alors F' qui est toujours entre M et A.

Retour à la page précédente ou fermer la page si elle a été ouverte séparément.

Menu général