Dans cette page on se propose de retrouver, par une construction géométrique, que l'ensemble des vecteurs orthogonaux à un vecteur x est un sous espace vectoriel, et qu'en terme affine, il est la direction de la tangente en le rayon vecteur unitaire porté par x. En formation, ces figures peuvent donc servir d'illustration du lien entre des considérations affines (la conjugaison) et vectorielles (l'orthogonalité)

Construction d'un vecteur orthogonal à x 

 

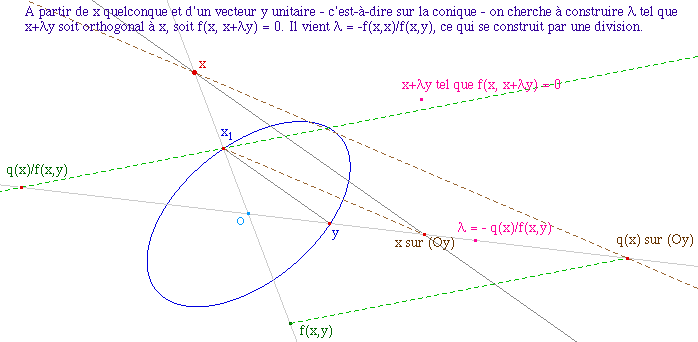
  OrthoFP1.fig

 

L'ensemble des vecteurs orthogonaux à x est un sev.

 

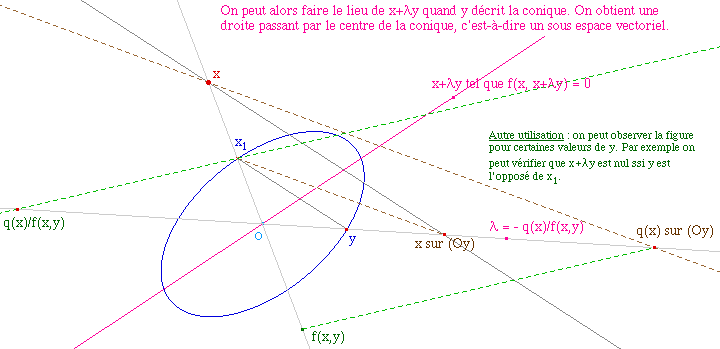
OrthoFP2.fig

Ce sev dirige la tangente au rayon vecteur associé à x

 

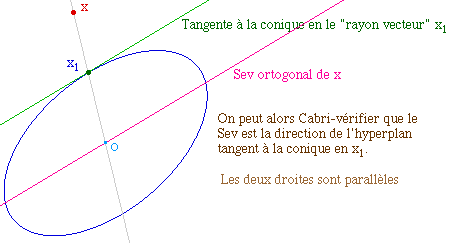
OrthoFP3.fig

 

 

Forme polaire associée | Exploration sur l'orthogonalité | Application à la dimension 3

[Groupe linéaire] [Réduction des endomorphismes] [Adjoint d'un endomorphisme] [Diago. simultannée]

[Retour Géométrie Vectorielle]

Menu général