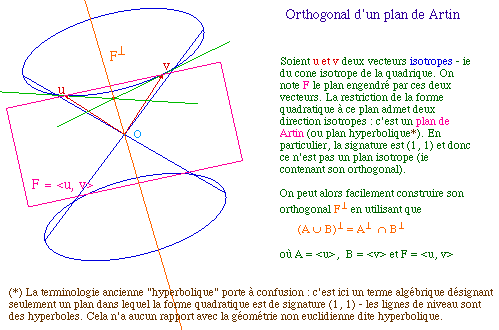
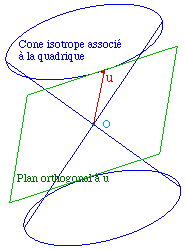
Considérons la quadrique q(u) = x²+y²-z², de signature (2, 1). Elle est non dégénérée, mais aussi non définie positive. Le cone isotrope est ... un cone affine.

Soit alors u un vecteur isotrope (u un "point" du cone). D'aprés ce qui précède, le plan orthogonal à u est tangent au cone en u. Et comme u est isotrope, il contient aussi u et il est ainsi entièrement déterminé.

Isotrop1.fig