Centre d'Euler d'un quadrilatère

4 - Cas du quadrilatère inscrit

[1 - Définition et propriétés] [2 Preuve de l'existence]
[3 - Preuve du centre d'une hyperbole équilatère] [5 - Itération de la construction]
[Retour Angle / Cocyclicité] [Retour Géométrie 2D] [Menu Général]

Cocyclicité des centres d'Euler | G milieu de E et O | Quadrilatère homothétique | Remarques complémentaires

Cocyclicité des centres des cercles d'Euler

Si le quadrilatère ABCD est inscrit dans un cercle de centre O et de rayon R, alors les centres des cercles d'Euler des triangles ABC, BCD, CDA, DAB sont cocycliques sur un cercle centré sur le centre d'Euler E du quadrilatère.

En effet, les cercles d'Euler est de rayon la moitié de celui du cercle circonscrit commun aux 4 triangles. Autrement dit le point E, commun aux 4 cercles, est à la distance R/2 de chacun des centres. Et donc ces centres sont sur le cercle de centre E et de rayon R/2.

Euler03.fig

De plus, E et O sont symétriques par rapport à l'isobarycentre G du quadrilatère. C'est ce que nous allons voir maintenant.

E et O symétriques par rapport à l'isobarycentre G

Cocyclicité des centres d'Euler | G milieu de E et O | Quadrilatère homothétique | Remarques complémentaires

L'homothétie de centre D de rapport 1/2 transforme le cercle circonscrit au quadrilatère en le cercle circonscrit à L, V, K et D.

Ce cercle (rose ci-contre) passe par O, image du symétrique de D par rapport à O.

Le symétrique de ce cercle, par rapport à l'isobarycentre G du quadrilatère est le cercle d'Euler du triangle ABC puisque que c'est le cercle circonscrit à I, J, U.

Ce cercle d'Euler contient donc le symétrique du centre du cercle circonscrit O du quadrilatère.

De même l'homothétie de centre A de rapport 1/2 transforme le cercle circonscrit au quadrilatère en le cercle circonscrit à L, U, I et A.

Ce cercle (rose ci-contre) passe par O, image du symétrique de A par rapport à O.

Le symétrique de ce cercle, par rapport à l'isobarycentre G du quadrilatère est le cercle d'Euler du triangle BCD puisque que c'est le cercle circonscrit à J, K, V. Comme ci-dessus, ce cercle d'Euler contient donc le symétrique du centre du cercle circonscrit O du quadrilatère.

Autrement dit les deux cercle d'Euler de ABC et BCD ont en commun les symétriques par rapport à G de L et de O, c'est à dire J et E puisque ces deux cercles se coupent en J et E. Puisque J est le symétrique de L par rapport à G, cela signifie que E est le symétrique de O par rapport à G.

Euler05.fig

Le quadrilatère des centres est homothétique du quadrilatère initial

Cocyclicité des centres d'Euler | G milieu de E et O | Quadrilatère homothétique | Remarques complémentaires

Mais poursuivons dans l'analyse de cette figure. Notons R et S les centres des cercles homothétiques du cercle circonscrit au quadrilatère dans les homothéties de centre A et D et de rapport 1/2. O, on l'a déjà dit, appartient à ces cercles comme images de A' et D'- diamétralement apposés à A et D sur le cercle circonscrit - dans ces homothéties.

Cela signifie que [AO] et [DO] sont des diamètres de ces cercles, et donc que RS = AD/2 dans le triangle AOD.

Mais puisque ces cercles, circonscrits respectivement à I, U, L et L, V, K, ont pour image les cercles d'Euler de centre O₂ et O₃ dans la symétrie centrale de centre G, cela signifie que [O₃O₂] est homothétique de [AD] dans une homothétie de rapport -1/2.

Euler06.fig

Et par extension à tous les côtés que le quadrilatère des centres d'Euler est homothétique du quadrilatère initial dans une homothétie de rapport -1/2.

Le centre H de cette homothétie (voir ci-dessous) est le point de (GO) tel que GH = - GO/3 (en écriture vectorielle). Chacun le vérifiera facilement par composition d'homothétie.

Euler06b.fig

Le quadrilatère des centres est homothétique dans une homothétie de rapport -1/2

Remarques complémentaires (dues à Géry Huvent)

Cocyclicité des centres d'Euler | G milieu de E et O | Quadrilatère homothétique | Remarques complémentaires

Cette configuration est décidément bien riche. Un collègue de Lille, Géry Huvent, en même temps que de proposer à abraCAdaBRI une preuve géométrique du fait que E est centre de l'hyperbole, nous propose ses remarques concernant ce cas particulier du quadrilatère inscrit.

Tout d'abord, si on note, pour i = 1, ..., 4, E_i l'homothétique de O_i dans l'homothétie de centre E de rapport 2, il est clair que les 4 points E_i sont cocycliques sur un cercle de centre E et de rayon R, le rayon du cercle circonscrit au quadrilatère. Par ailleurs, par construction même, ce cercle C' est tangent aux 4 cercles d'Euler de centres O_i puisque E, Oi et E_i sont alignés.

Euler03b.fig
D'aprés ce qui précède, ce cercle C' est le translaté du cercle circonscrit C dans la translation de vecteur OE, c'est aussi le symétrique de C dans la symétrie de centre G.

Avec les notations précédentes, remarquons que le cercle d'Euler de ABC - de centre O₂ - est l'homothétique du cercle circonscrit C dans l'homothétie de centre H, l'orthocentre de ABC - ci-dessous H_ABC - et de rapport 1/2. En effet, on sait que le centre du cercle d'Euler est le milieu de l'orthocentre et du centre du cercle circonscrit.

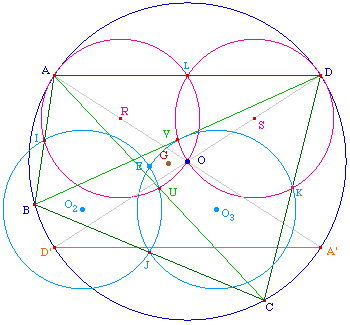
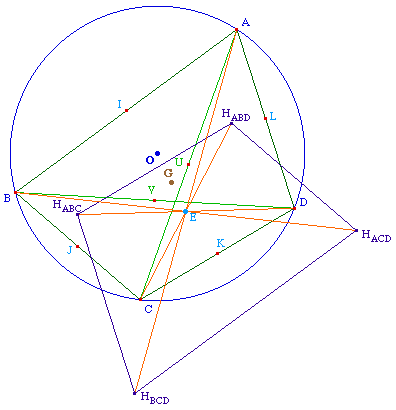
Montrons alors, que dans cette homothétie, l'image du quatrième point du quadrilatère, le point D, n'est autre que le centre d'Euler du quadrilatère.

Euler07.fig

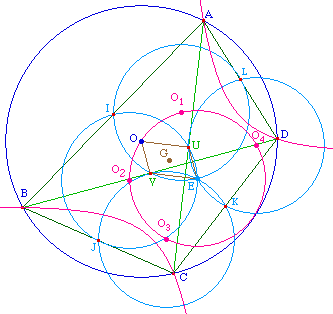
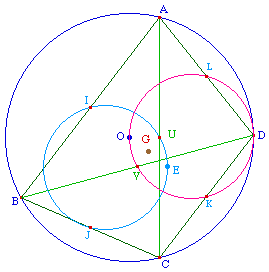
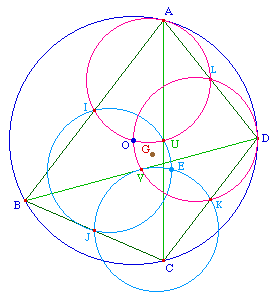
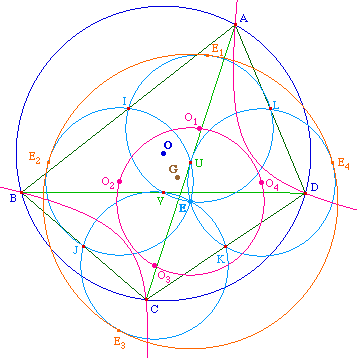
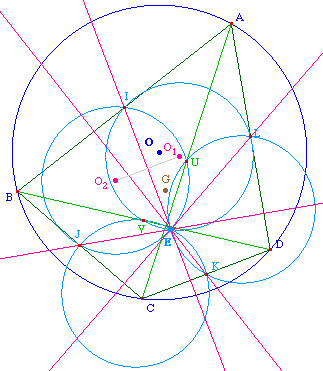
Soit M ce point : M = h_H,1/2(D). Il est sur le cercle d'Euler de ABC, soit sur le cercle circonscrit à IJU. En angle de droites on peut donc écrire (MV, MJ) = (IV, IJ).
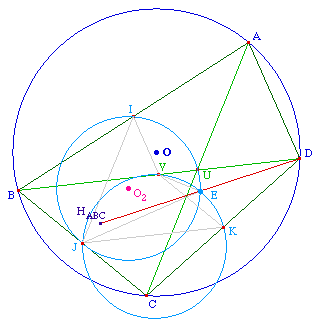
Par ailleurs (IV, IJ) = (AD, AC) = (BD, BC) car A, B, C, D sont cocycliques. Comme (BD, BC) = (KV, KJ), on a : (MV, MJ) = (KV, KJ) et donc M est aussi sur le cercle circonscrit à JKV soit sur le cercle d'Euler de BCD. Or ces deux cercles d'Euler ont J en commun et se recoupent en E, et ainsi M = E.

En consèquence, le quadrilatère des orthocentres des quatre triangles est le symétrique de ABCD par rapport à E. Il lui est donc isométrique.

Euler08.fig
Ces 4 points sont bien entendu sur l'hyperbole équilatère passant par A, B, C et D.

Les mi-hauteurs d'un quadrilatère inscrit

Géry Huvent nous fait joliment remarquer que la propriété de l'item précédent (quadrilatère homothétiques) permet de retrouver une propriété connue sous le nom de "mi-hauteurs du quadrilatère inscrit", à savoir :

Dans un quadrilatère inscrit, les quatre droites passant par le milieu d'un côté et perpendiculaire au côté opposé sont concourantes en un point E symétrique du cercle circonscrit par rapport à l'isobarycentre du quadrilatère.

Euler10.fig

Vu ce qui précède la preuve est assez immédiate. Considérons la droite passant par I milieu de [AB] et perpendiculaire à [CD]. Cette droite est aussi perpendiculaire à [O₁O₂] car on a vu que O₁O₂O₃O₄ est homothétique de DCBA et en particulier (O₁O₂) // (CD).

Comme I est commun aux deux cercles d'Euler de centre O₁ et O₂, la perpendiculaire que l'on considère ici, perpendiculaire à la droite des centres, n'est autre que l'axe radical des deux cercles. Elle passe donc par l'autre point d'intersection E de ces cercles.

De même pour les autres droites, et ainsi les 4 perpendiculaires passent par le centre d'Euler.

Remarque : une preuve directe de ce résultat est en même temps une autre preuve de l'existence du centre d'Euler d'un quadrilatère. Dans ce dossier , comme c'est son thème, nous avons favorisé la cocyclicité.

Cocyclicité des centres d'Euler | G milieu de E et O | Quadrilatère homothétique | Remarques complémentaires

[1 - Définition et propriétés] [2 Preuve de l'existence]
[3 - Preuve du centre d'une hyperbole équilatère] [5 - Itération de la construction]

[Retour Angle / Cocyclicité] [Retour Géométrie 2D]

Cocyclicité des centres des cercles d'Euler

Si le quadrilatère ABCD est inscrit dans un cercle de centre O et de rayon R, alors les centres des cercles d'Euler des triangles ABC, BCD, CDA, DAB sont cocycliques sur un cercle centré sur le centre d'Euler E du quadrilatère.

En effet, les cercles d'Euler est de rayon la moitié de celui du cercle circonscrit commun aux 4 triangles. Autrement dit le point E, commun aux 4 cercles, est à la distance R/2 de chacun des centres. Et donc ces centres sont sur le cercle de centre E et de rayon R/2.

De plus, E et O sont symétriques par rapport à l'isobarycentre G du quadrilatère. C'est ce que nous allons voir maintenant.

E et O symétriques par rapport à l'isobarycentre G

L'homothétie de centre D de rapport 1/2 transforme le cercle circonscrit au quadrilatère en le cercle circonscrit à L, V, K et D.

Ce cercle (rose ci-contre) passe par O, image du symétrique de D par rapport à O.

Le symétrique de ce cercle, par rapport à l'isobarycentre G du quadrilatère est le cercle d'Euler du triangle ABC puisque que c'est le cercle circonscrit à I, J, U.

Ce cercle d'Euler contient donc le symétrique du centre du cercle circonscrit O du quadrilatère.

De même l'homothétie de centre A de rapport 1/2 transforme le cercle circonscrit au quadrilatère en le cercle circonscrit à L, U, I et A.

Ce cercle (rose ci-contre) passe par O, image du symétrique de A par rapport à O.

Le symétrique de ce cercle, par rapport à l'isobarycentre G du quadrilatère est le cercle d'Euler du triangle BCD puisque que c'est le cercle circonscrit à J, K, V. Comme ci-dessus, ce cercle d'Euler contient donc le symétrique du centre du cercle circonscrit O du quadrilatère.

Autrement dit les deux cercle d'Euler de ABC et BCD ont en commun les symétriques par rapport à G de L et de O, c'est à dire J et E puisque ces deux cercles se coupent en J et E. Puisque J est le symétrique de L par rapport à G, cela signifie que E est le symétrique de O par rapport à G.

Le quadrilatère des centres est homothétique du quadrilatère initial

Cela signifie que [AO] et [DO] sont des diamètres de ces cercles, et donc que RS = AD/2 dans le triangle AOD.

Mais puisque ces cercles, circonscrits respectivement à I, U, L et L, V, K, ont pour image les cercles d'Euler de centre O2 et O3 dans la symétrie centrale de centre G, cela signifie que [O3O2] est homothétique de [AD] dans une homothétie de rapport -1/2.

Et par extension à tous les côtés que le quadrilatère des centres d'Euler est homothétique du quadrilatère initial dans une homothétie de rapport -1/2.

Le centre H de cette homothétie (voir ci-dessous) est le point de (GO) tel que GH = - GO/3 (en écriture vectorielle). Chacun le vérifiera facilement par composition d'homothétie.

Remarques complémentaires (dues à Géry Huvent)

D'aprés ce qui précède, ce cercle C' est le translaté du cercle circonscrit C dans la translation de vecteur OE, c'est aussi le symétrique de C dans la symétrie de centre G.

Montrons alors, que dans cette homothétie, l'image du quatrième point du quadrilatère, le point D, n'est autre que le centre d'Euler du quadrilatère.

En consèquence, le quadrilatère des orthocentres des quatre triangles est le symétrique de ABCD par rapport à E. Il lui est donc isométrique.

Ces 4 points sont bien entendu sur l'hyperbole équilatère passant par A, B, C et D.

Les mi-hauteurs d'un quadrilatère inscrit

Géry Huvent nous fait joliment remarquer que la propriété de l'item précédent (quadrilatère homothétiques) permet de retrouver une propriété connue sous le nom de "mi-hauteurs du quadrilatère inscrit", à savoir :

Dans un quadrilatère inscrit, les quatre droites passant par le milieu d'un côté et perpendiculaire au côté opposé sont concourantes en un point E symétrique du cercle circonscrit par rapport à l'isobarycentre du quadrilatère.

Vu ce qui précède la preuve est assez immédiate. Considérons la droite passant par I milieu de [AB] et perpendiculaire à [CD]. Cette droite est aussi perpendiculaire à [O1O2] car on a vu que O1O2O3O4 est homothétique de DCBA et en particulier (O1O2) // (CD).

Comme I est commun aux deux cercles d'Euler de centre O1 et O2, la perpendiculaire que l'on considère ici, perpendiculaire à la droite des centres, n'est autre que l'axe radical des deux cercles. Elle passe donc par l'autre point d'intersection E de ces cercles.

De même pour les autres droites, et ainsi les 4 perpendiculaires passent par le centre d'Euler.

Menu général

Mais puisque ces cercles, circonscrits respectivement à I, U, L et L, V, K, ont pour image les cercles d'Euler de centre O₂ et O₃ dans la symétrie centrale de centre G, cela signifie que [O₃O₂] est homothétique de [AD] dans une homothétie de rapport -1/2.

Vu ce qui précède la preuve est assez immédiate. Considérons la droite passant par I milieu de [AB] et perpendiculaire à [CD]. Cette droite est aussi perpendiculaire à [O₁O₂] car on a vu que O₁O₂O₃O₄ est homothétique de DCBA et en particulier (O₁O₂) // (CD).

Comme I est commun aux deux cercles d'Euler de centre O₁ et O₂, la perpendiculaire que l'on considère ici, perpendiculaire à la droite des centres, n'est autre que l'axe radical des deux cercles. Elle passe donc par l'autre point d'intersection E de ces cercles.