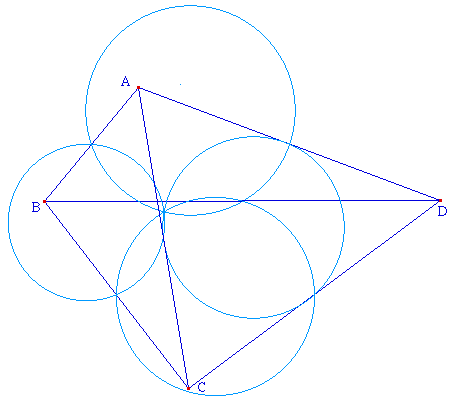
ABCD est un quadrilatère, I, J, K, L, U et V les mileiux des côtés et des diagonales comme ci-contre.

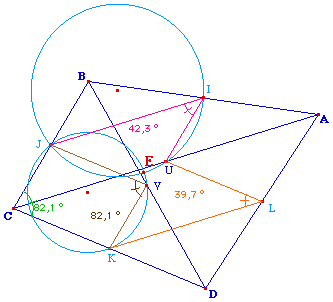
Soit E l'autre intersection que J des cercles d'Euler de ABC et BCD. E est différent de J car les triangles IJU et JKV sont de vrais triangles. On se propose de vérifier que E, U, K, L sont cocycliques, ce qui prouvera que le cercle d'Euler de ACD passe aussi par E. On ferait de même pour le quatrième cercle.

PreuveE1.fig

La preuve se fait avec des angles de droites - et non des angles géoémtriques ou de vecteur comme pourrait le laisser penser l'illustration : les arguments sont alors corrects même si le quadrilatère n'est pas convexe.

Pour éviter des lourdeurs d'écriture, on notera dans cette page (AB, CD) l'angle orienté des droites (AB) et (CD).

CUIJ et CKLU étant des parallèlogrammes, on a (par exemple par symétrie centrale) :

(CB, CA) = (IU, IJ) et (CD, CA) = (LU, LK)

De même on a (VJ, VK) = (CD, CB) car CKVJ est un parallélogramme.