Centre d'Euler d'un quadrilatère

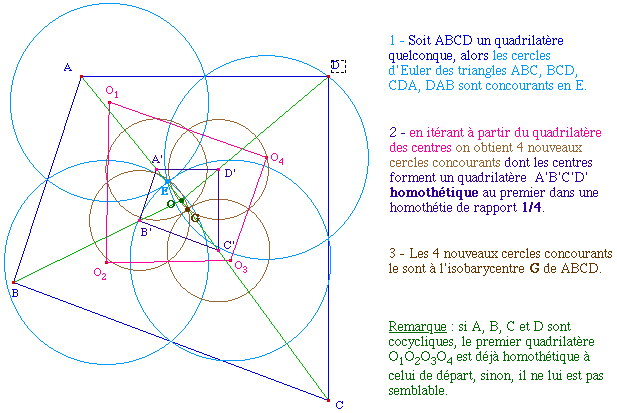
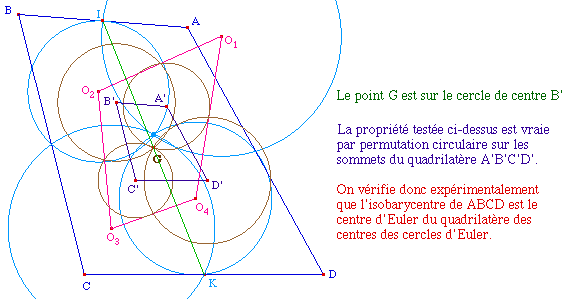
5 - Itération de la construction

[1 - Définition et propriétés] [2 Preuve de l'existence] [3 - Preuve du centre d'une hyperbole équilatère]
[4 - Preuve dans le cas du quadrilatère inscrit]

[Retour Angle / Cocyclicité] [Retour Géométrie 2D] [Menu Général]

 

 

Résultat général

En dehors du point 1, déjà vu, les autres résultats mentionnés ci-dessous sont, dans un premier temps, des Cabri-expérimentations. La remarque, elle, a été prouvée à la page 4. Les points 2 et 3 sont proposés à la tenacité des lecteurs. votre preuve peut compléter cette page. Contacter abraCAdaBRI.

 

EulerB1.fig

 

 

Non similitude de ABCD et O1O2O3O4 dans le cas général, et autres cas particuliers

 

Cas général (points non cocycliques)

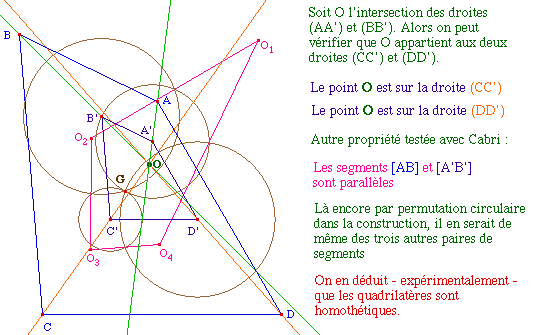
Pas de similitude, c'est clair

Cas cocyclique

Quadrilatères homothétiques (Preuve).

 

Cas non cocyclique : conservation de l'angle droit

Si le quadrilatère a 2 angles droits, cette conservation induit
une similitude indirecte entre les deux quadrilatères (ci-contre).

EulerB3.fig

 abraCAdaBRI est intéressé par vos preuves - géométriques - de ces deux résultats à priori surprenants.

 

 

Expérimentation sur l'itération du procédé.

Voici deux figures d'expérimentation sur les résultats annoncés, pour étudier une éventuelle preuve géométrique. Dans la première figure G est le milieu de [IK].

 

 

  EulerB4a.fig

 

 

EulerB4b.fig

 

 

 [1 - Définition et propriétés] [2 Preuve de l'existence] [3 - Preuve du centre d'une hyperbole équilatère]
[4 - Preuve dans le cas du quadrilatère inscrit]

[Retour Angle / Cocyclicité] [Retour Géométrie 2D]

Menu général