Centre d'Euler d'un
quadrilatère
3 - Centre de l'hyperbole
équilatère passant par A, B, C, D
[1 - Définition
et propriétés] [2
Preuve de l'existence]
[4 - Preuve dans le cas du
quadrilatère inscrit] [5
- Itération de la construction]
[Retour Angle /
Cocyclicité] [Retour
Géométrie 2D] [Menu
Général]
Principe de la preuve | Preuve
géométrique | Preuve
analytique | Compléments
Résultat et principe de la
preuve
|
|
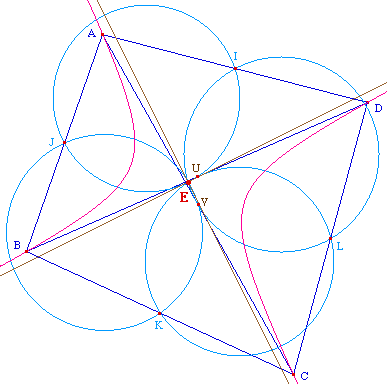
On se propose de montrer le résultat suivant
:
Le centre d'Euler d'un
quadrilatère ABCD est aussi le centre d'une hyperbole
équilatère passant par les 4 points A, B, C et
D.
 Euler02.fig
Euler02.fig
Pour cela, nous allons montrer un résultat
dû à Poncelet et Brianchon :
si une hyperbole
équilatère passe 3 points d'un triangle, alors
son centre est sur le cercle d'Euler du
triangle.
Il est clair que le résultat en
découle.
On notera que si le quadrilatère n'est pas
ortocentrique, l'hyperbole équilatère est
unique, sinon il y en a une infinité.
On peut également remarquer que le
quadrilatère des orthocentres est aussi sur
l'hyperbole.
|
Preuve
géométrique (proposée par
Géry
Huvent)
La preuve géométrique est plus longue que celle
analytique car nous commençons par montrer une
caractérisation angulaire de l'hyperbole
équilatère, alors que l'on ne remontre pas
l'équation réduite de l'hyperbole ramenée
à ses asymptotes.
Principe de la preuve
| Preuve géométrique | Preuve
analytique | Compléments
Vous pouvez charger l'article complet de Géry
Huvent - avec preuve des rappels et des compléments non
développés ici - dans les deux formats OrthocentreGH.dvi
(16 Ko) ou orthocentreGH.PDF
(206 Ko), les deux contenant les
illustrations.
|
 PropHypG.fig
PropHypG.fig
|
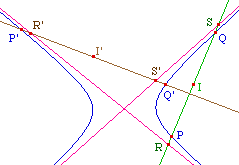
On suppose connue cette propriété
générale des sécantes aux hyperboles et
à leurs asymptotes :
Si une droite d coupe une
hyperbole en P et Q, et ses asymptotes en R et S, alors
[PQ] et [RS] ont même
milieu.
Rappelons que cette propriété permet par
exemple de construire avec Cabri une hyperbole connaissant
ses asymptotes et un point, ce que l'on a déjà
utilisé plusieurs fois dans abraCAdaBRI.
Cette propriété, affine, permet quelques
développements intéressants dans le cas
particulier - euclidien - où l'hyperbole est
équilatère : les asymptotes étant
orthogonales ...
|
Caractérisation
angulaire de l'hyperbole équilatère
 PropHE01.fig
PropHE01.fig
|
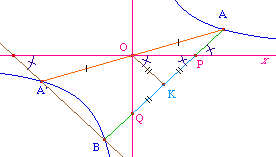
Sens direct
On considère une hyperbole
équilatère de centre O passant A. A' est le
symétrique de A par rapport à O et B un autre
point de l'hyperbole. La droite (AB) coupe les asymptotes en
P et Q.
POQ est rectangle en O. Soit K le milieu de [AB]
Par le théorème des milieux (ou Thalès)
(OK) // (A'B). Or comme K est aussi milieu de [PQ],
c'est le centre du cercle circonscrit à POQ, et donc
le triangle KPO est isocèle en K.
On en déduit la relation angulaire (en angles de
droites) :
(Ox, AB) = (A'B,
Ox)
|
Sens
réciproque
On considère l'hyperbole équilatère de
diamètre (AA') et d'asymptote (Ox)
Soit M un point (différent de A et de A') tel que
(Ox, AM) = (A'M, Ox). Alors la
droite (AM) coupe l'hyperbole en un autre point B
(différent de A') qui vérifie la même
propriété angulaire d'après le sens direct
: (Ox, AB) = (A'B, Ox). Puisque M
appartient à la droite (AB), on a alors les
égalités d'angles de droites : (A'M, Ox) = (Ox,
AM) = (Ox, AB) = (A'B, Ox).
Il en résulte que (A'M) = (A'B). Comme
déjà (AM) = (AB), M est à l'intersection
des droites (A'B) et (AB), M est le point B, et donc M
appartient à l'hyperbole équilatère.
D'où la caractérisation :
Un point M est sur l'hyperbole
équilatère de diamètre [AA'] et
d'asymptote (Ox) ssi (Ox, AM) = (A'M, Ox).
Deux conséquences à cette
caractérisation
 PropHE02.fig
PropHE02.fig
|
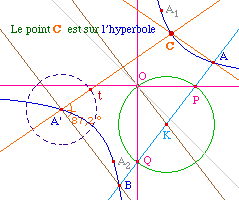
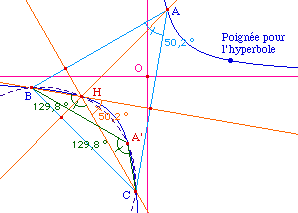
Corollaire 1 :
Le lieu des point C tels que (AB,
AC) = (A'C, A'B) - en angles de droites - est l'hyperbole
équilatère de diamètre [AA']
passant par B.
Construction ci-contre :
à partir de A, A', et B on peut constuire les
asymptotes (par K, P et Q), puis deux autres points de
l'hyperbole A1 et A2. Sur un cercle
centré en A, un paramètre t permet de
construire tous les points C tel que (AB, AC) = (A'C, A'B).
On vérifie alors - par le vérificateur de
propriété de Cabri - que C est sur
l'hyperbole.
On aurait pu faire une figure donnant le lieu de C et
vérifier que c'est une hyperbole
équilatère de centre le milieu de
[AA'], passant par les trois points A, A' et B.
Preuve : par la relation de Chasles sur les angles de
droites, en utilisant la relation angulaire pour B.
|
 PropHE03.fig
PropHE03.fig
|
Corollaire 2 :
L'orthocentre H d'un triangle ABC
inscrit dans une hyperbole équilatère
appartient à cette hyperbole.
Preuve : (HC, HB) = (AB, AC) par angles à
côtés perpendiculaires. Et donc d'après
le corollaire précédent (HC) = (HB) = (A'C,
A'B) : les 4 points B, H, A', C sont
cocycliques. Il en résulte que (A'H, A'B) =
(CH, CB). Or (CH, CB) = (AB, AH) par angles à
côtés perpendiculaires, d'où (A'H, A'B)
= (AB, AH). Soit, d'après le corollaire ci-dessus : H
appartient à l'hyperbole équilatère de
diamètre [AA'] passant par B,
c'est-à-dire l'hyperbole équilatère de
départ.
Remarque : comme on sait que le symétrique
de l'orthocentre par rapport à un côté
est sur le cercle circonscrit au triangle, le cercle
circonscrit à B, C et H est le symétrique du
cercle circonscrit à ABC par rapport à (BC).
|
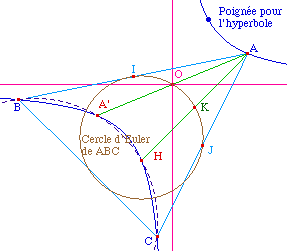
Preuve de l'appartenance du
centre de l'hyperbole au cercle d'Euler d'un triangle
inscrit
 PropHE04.fig
PropHE04.fig
|
L'homothétie de centre A et de rapport 1/2
transforme B et C en les milieux I et J des
côtés [AB] et [AC]. Elle
transforme H en le milieu K de [AH].
Or le cercle circonscrit à I, J, et K n'est rien
d'autre que le cercle d'Euler (dit aussi "des 9 points") du
triangle ABC.
Comme on vient de voir à la figure
précédente que B, A', H et C sont cocyclique,
par homothétie, le milieu O de [AA']
appartient au cercle d'Euler.
Et ainsi :
Le centre d'un hyperbole
équilatère est sur le cercle d'Euler de tout
triangle inscrit dans cette hyperbole.
Ceci suffit à prover que le centre d'Euler d'un
quadrilatère est le centre de l'hyperbole
équilatère passant par ces quatre points.
|
Signalons que Géry
Huvent a proposé d'autres conséquences dans son
article, qui seront mises en ligne ultérieurement dans
abraCAdaBRI. Il a aussi proposé d'autres
commentaires sur le cas particulier où le
quadrilatère ABCD est incriptible dans un cercle.
Preuve analytique
(proposée par Pierre
Delezoïde)
Principe de la
preuve | Preuve géométrique |
Preuve analytique | Compléments
|
 CHypEul1.fig
CHypEul1.fig
|
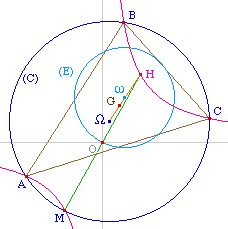
ABC est un triangle de centre de cercle circonscrit
"Oméga" (W dans la suite du texte), d'isobarycentre G
d'orthocentre H. On note "oméga" (w dans la suite) le
centre du cercle d'Euler. Soit (H) une hyperbole
équilatère passant par A, B, et C. Notons O
son centre. (H) recoupe le cercle circonscrit (C) en un
quatrième point M.
Dans un repère normé de centre O dont les
axes sont les asymptotes de (H), l'équation de (H)
est xy = a. Puisqu'elle est
équilatère, le repère est
orthonormé et donc l'équation du cercle (C)
est de la forme : x2 +
y2 - 2ux -2vy + c = 0. Son centre W est
donc de coordonnées (u, v).
En écrivant y = a/x, l'équation de
l'intersection (du 4° degré) en x, il est facile
d'en déduire que la somme des abscisses des 4
intersections est 2u (par le
coefficient de X3). De même en
écrivant x = a/y, on en déduit que la somme
des ordonnées des 4 intersections est
2v. Il en résulte alors
que :
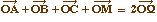 Et donc
Et donc 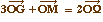
En utilisant la relation d'Euler 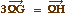 on arrive à
on arrive à 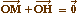
Et donc M et H sont symétriques dans la
symétrique de centre O, centre de l'hyperbole.
|
Remarque : cette
première partie montre en même temps que
l'orthocentre d'un triangle formé de trois points d'une
hyperbole équilatère appartient à cette
hyperbole.
On sait de plus que w est milieu de [HW], ou encore
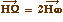 . Et
donc l'homothétie de centre H et de rapport 1/2 transforme le
cercle circonscrit (C) en le cercle d'Euler (E). Dans cette
homothétie, O est l'image de M, et ainsi :
. Et
donc l'homothétie de centre H et de rapport 1/2 transforme le
cercle circonscrit (C) en le cercle d'Euler (E). Dans cette
homothétie, O est l'image de M, et ainsi :
Le cente d'une hyperbole
équilatère passant par trois points ABC appartient au
cercle d'Euler de ce triangle.
On a alors vu qu'il en résultait que le centre d'Euler
d'un quadrilatère est le centre de l'hyperbole
équilatère passant par ces 4 points.
Illustration d'une
remarque précédente et complément
Principe de la preuve
| Preuve géométrique | Preuve
analytique | Compléments
Le quadrilatère des orthocentres admet la même
hyperbole, puisque l'orthocentre d'un triangle de 3 points d'une
hyperbole équilatère est un point de l'hyperbole.
Ci-dessous les commentaires sont ceux de l'item "Appartenance" de
Cabri.
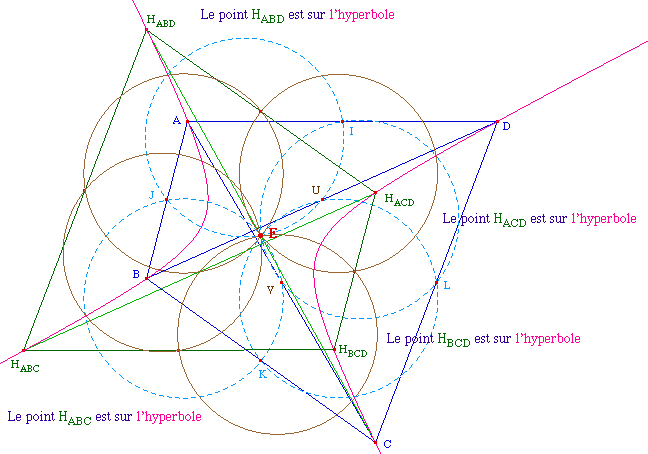
 Euler04.fig
Euler04.fig
On peut observer également la propriété
suivante (commentaires des items "Propriétés" de
Cabri), que nous montrerons avec les résultats de la
page 4 (ci dessous D est redéfini comme appartenant au
cercle circonscrit à ABC) :
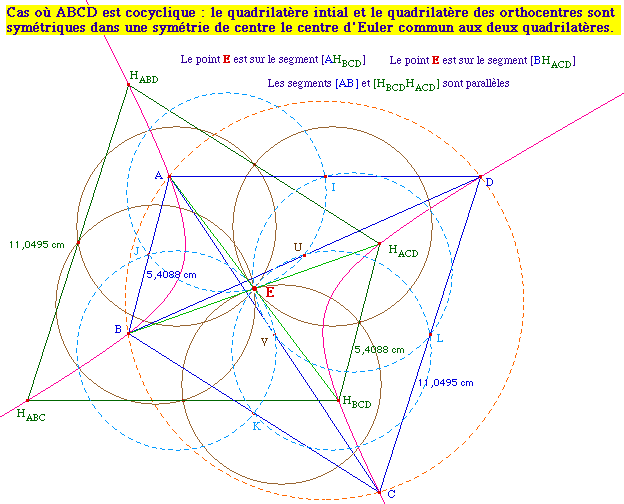
Principe de la preuve |
Preuve géométrique | Preuve
analytique | Compléments
[1 - Définition
et propriétés] [2
Preuve de l'existence]
[4 - Preuve dans le cas du
quadrilatère inscrit] [5
- Itération de la construction]
[Retour Angle /
Cocyclicité] [Retour
Géométrie 2D]
 Menu
général
Menu
général








