[2 Preuve de l'existence] [3 - Preuve du centre d'une hyperbole équilatère]
[4 - Preuve dans le cas du quadrilatère inscrit] [5 - Itération de la construction]

[Retour Angle / Cocyclicité] [Retour Géométrie 2D] [Menu Général]

 

Cette page est à prendre comme un exercice, décrit en trois illustrations, relatif au quadrilatère et utilisant la cocyclicité. Les pages suivantes (2 à 4) contiennent les solutions, la dernière étant un prolongement les preuves étant à proposer à abraCAdaBRI.

Existence

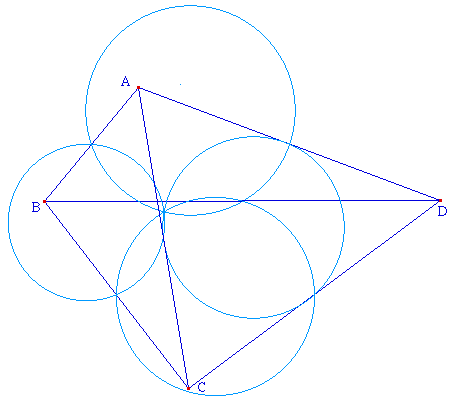
Soit ABCD un quadrilatère, alors les cercles d'Euler des triangles ABC, BCD, CDA, DAB sont concourants en un point appelé centre d'Euler du quadrilatère ABCD.

 

Euler01.fig

 

Propriété

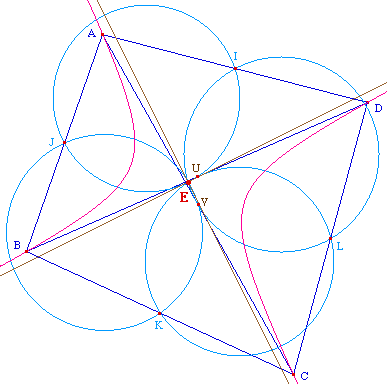
Le centre d'Euler d'un quadrilatère ABCD est aussi le centre de l'hyperbole équilatère - en général elle est unique - passant par les 4 points A, B, C et D.

Euler02.fig

 

Cas d'un quadrilatère inscrit

 

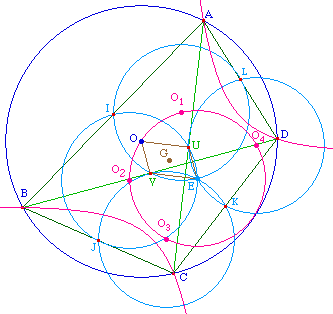
Si le quadrilatère ABCD est inscrit dans un cercle de centre O, alors les centres O_i des cercles d'Euler des triangles ABC, BCD, CDA, DAB sont cocycliques sur un cercle centré sur le centre d'Euler E du quadrilatère.

De plus, E et O sont symétriques par rapport à l'isobarycentre G du quadrilatère.

Euler03.fig

[2 Preuve de l'existence] [3 - Preuve du centre d'une hyperbole équilatère]
[4 - Preuve dans le cas du quadrilatère inscrit] [5 - Itération de la construction]

Menu général