[Preuve géométrique]

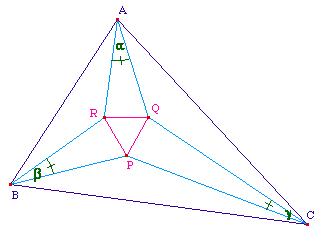
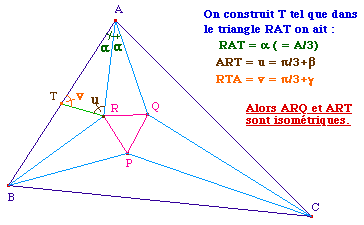
La preuve proposée ci-dessous est celle de Claude Tisseron dans son ouvrage de référence sur les géométries affine, euclidienne et projective. (voir la page 7 pour les références) On trissecte donc les angles d'un triangle, avec les notations ci-contre. L'idée est de calculer RQ en fonction de A/3, B/3, C/3. On montre alors que l'expression de RQ est symétrique en A/3, B/3 et C/3. Donc PQR sera équilatéral du fait que ces côtés sont de même longueur. On notera R le rayon du cercle circonscrit à ABC.

Lemme technique (cette partie est traitée avec des variantes selon les preuves proposées en page 7. Voir plus loin pour une variante n'utilisant pas ce lemme)

Remarquer que pour et deux réels compris strictement entre 0 et Pi de somme inférieure à Pi, et pour et positifs, on a

Premiers calculs (utilisant la "formule des sinus")

Montrer que, avec les notation ci-dessus, on a

Transformation des calculs

En utilisant que sin 3x = 3 sin x - 4sin³x, transformer les expressions en :

Conclusion

Utiliser le lemme pour en déduire que et conclure que le triangle est équilatéral.

Remarque

Des variantes de la preuve utilisent directement que ce que l'on montre en fait dans la seconde partie.

Variante

Une autre version, proposée par Jean Fresnel (voir les références page 7) consiste à construire un point T de [AB] vérifiant les relations détaillées ci-contre. Il est alors facile de montrer, par la formule des sinus, que AT = AR. Il en résulte - cas "d'égalité des triangles" - que les triangles ARQ et ATR sont isométriques, ou encore que T est le symétrique de Q par rapport à (AR). On connait donc les angles de ARQ. On en déduit alors RQ et on conclu comme ci-dessus.

  [Preuve géométrique]

Menu général