[Preuve trigonométrique]

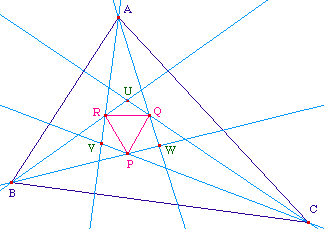
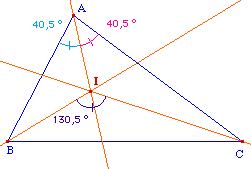
La preuve proposée ci-dessous est celle proposée par Jean Marie Monier dans son ouvrage d'exercices. (voir la page 7 pour les références) L'idée est de remarquer que si PQR est équilatéral, alors URQ est isocèle. Ensuite, partant d'un triangle équilatéral, on construit, sur cette base, un triangle semblable à un triangle ABC de départ où P, Q et R sont les intersections des trissectrices. On conclu par similitude. MRLPGeo.fig (ici on part d'un triangle ABC)

1 - Lemme : une caractérisation du centre du cercle inscrit à un triangle

 2 - Avec un triangle équilatéral

Les notations sont celles de la figure ci-dessus, mais les points de base seraient P, Q, R et U, V, W

Soient trois nombres a, b, c, compris entre 0 et Pi/3, strictement, de somme égale à 2Pi/3.

Soit PQR un triangle équilatéral et sur les côtés de ce triangle, à l'extérieur, U, V, W tels que URQ, VPR et WQP soient isocèles, d'angles à la base, respectivement a, b, et c. On note A l'intersection des droites (RV) et (QW), B celle des droites (UR) et (PW) et C celle de (UQ) et (VP).

1.a. Montrer que

2. En déduire que P est le centre du cercle inscrit du triangle BUC.

3. Conclure que les droites (AR), (AQ), (BP), (BR), (CQ) et (CR) sont les trissectrices intérieures de angles géométriques du triangle ABC.

2 - Application : Le théorème de Morley

En déduire, comme indiqué dans la présentation que les trissectrices (intérieures) adjacentes d'un triangle quelconque sont sécantes en des points qui forment un triangle équilatéral.

Selon Jean Marie Mounier, cette preuve - particulièrement élégante - est de Raoul Bricard, et date de 1922.

  [Preuve trigonométrique]

Menu général