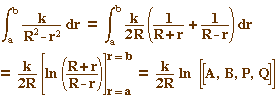2 - Un monde non euclidien selon Poincaré

Le texte de Henri Poincaré (extrait de "La science et l'hypothèse" - Chap. 4 : L'espace et la géométrie - 1908)

Si l'espace géométrique était un cadre imposé à chacune de nos représentations, considérée individuellement, il serait impossible de se représenter une image dépouillée de ce cadre, et nous ne pourrions rien changer à notre géométrie. Mais il n'en n'est pas ainsi, la géométrie n'est que le résumé des lois suivant lesquelles se succèdent ces images. Rien n'empêche alors d'imaginer une série de représentations de tout point semblables à nos représentations ordinaires, mais se succédant d'après des lois différentes de celles auxquelles nous sommes accoutumés. On conçoit alors que des êtres dont l'éducation se ferait dans un milieu où ces lois seraient ainsi bouleversées pourraient avoir une géométrie très différente de la nôtre. Supposons par exemple un monde renfermé dans une grande sphère et soumis aux lois suivantes :

La température n'y est pas uniforme; elle est maxima au centre, et elle diminue à mesure qu'on s'en éloigne, pour se réduire au zéro absolu quand on atteint la sphère où ce monde est renfermé. Je précise davantage la loi suivant laquelle varie cette température. Soit R le rayon de la sphère limite; soit r la distance du point considéré au centre de cette sphère.
La température absolue sera proportionnelle à R²-r². Je supposerai de plus que, dans ce monde, tous les corps aient même coefficient de dilatation, de telle façon que la longueur d'une règle quelconque soit poportionnelle à sa température absolue.Je supposerai enfin qu'un objet transportéd'un point à un autre, dont la température est différente, se met immédiatement en équilibre calorifique avec son nouveau milieu. Rien dans ces hypothèses n'est contradictoire ou inimaginable.

Un objet mobile deviendra alors de plus en plus petit à mesure qu'on se rapprochera de la sphère limite. Observons d'abord que, si ce monde est limité au point de vue de notre géométrie habituelle, il paraîtra infini à ses habitants. Quand ceux-ci, en effet, veulent se rapporcher de la sphère limite, ils se refroidissent et deviennent de plus en plus petits. Les pas qu'ils font sont donc aussi de plus en plus petits, de sorte qu'ils ne peuvent jamais attendre la sphère limite.

Si, pour nous, la géométrie n'est que l'étude des lois suivant lesquelles se meuvent les solides invariables, pour ces êtres imaginaires, ce sera l'étude des lois suivant lesquelles se meuvent les solides déformés par ces différences de température dont je viens de parler. Sans doute, dans notre monde, les solides naturels éprouvent également des variations de forme et de volume dues à l'échaffement ou au refroidissement. Mais nous négligeons ces variations en jetant les fondements de la géométrie; car, outre qu'elles sont très faibles, elles sont irrégulières et nous paraissent par conséquent accidentelles. Dans ce monde hypothètique, il n'en serait plus de même, et ces variations suivraient des lois régulières et trés simples. D'autre part, les diverses pièces solides dont se composerait le corps de ses habitants, subiraient les mêmes variations de forme et de volume.

Je ferais une autre hypothèse; je supposerai que la lumière traverse des milieux diversement réfringents et de telle sorte que l'indice de réfraction soit inversement proportionnel à R²-r². Il est aisé de voir que, dans ces conditions, les rayons lumineux ne seraient pas rectilignes, mais circulaires. Pour justifier ce qui précède, il me reste à montrer que certains changements survenus dans la position des objets extérieurs peuvent être corrigés par des mouvements corrélatifs des êtres sentant qui habitent ce monde imaginaire; et cela de façon à restaurer l'ensemble primitif des impression subies par ces êtres sentants.

Supposons en effet, qu'un objet se déplace, en se déformant, non comme un solide invariable, mais comme un solide éprouvant des dilatations inégales, exatement conformes à la loi de température que j'ai supposée plus haut. Qu'on me permette, pour abréger le langage, d'appeler un pareil mouvement déplacement non euclidien.

Si un être sentnat se trouve dans le voisinage, ses impressions seront modifiées par le déplacement de l'objet, mais il pourra les rétablir en se mouvant lui-même d'une manière convenable. Il suffit que finalement l'ensemble de l'objet et de l'être sentant, considéré comme un seul corps, ait éprouvé un de ces déplacements particuliers que je viens d'appeler non euclidien. Cela est possible si l'on suppose que les membres de ces être se dilatent d'après la même loi que les autres corps du monde qu'ils habitent.

Bien qu'ua point de vue de notre géométrie habituelle les corps se soient déformés dans ce déplacement et que leurs diverses parties ne se retrouvent plus dans la même situation relative, cepandant nous allons voir que les impressions de l'être sentant sont redevenues les mêmes. En effet, si les distances mutuelles des diverses parties ont pu varier, néanmoins les parties primitivement en contact sont revenues en contact. Les impressions tactiles n'ont donc pas changées. D'autre part, en tenant compte de l'hypothèse faite plus haut au sujet de la réfraction et de la courbure des rayons lumineux, les impressions visuelles seront aussi restées les mêmes.

Ces êtres imaginaires seront donc, comme nous, conduits à classer les phénomènes dont ils seront témoins et à distinguer parmi eux, les "cangements de position" succeptibles d'être corrigés par un mouvement relatif corrélatif. S'ils fondent une géométrie, ce ne sera pas, comme la nôtre, l'étude des mouvements de nos solides invariables; ce sera celle des changements de position qu'ils auront ainsi distingués, et qui ne sont autres que les déplacements non euclidiens : ce sera une géométrie non euclidienne.

Ainsi, des êtres comme nous, dont l'éducation se ferait dans un pareil monde, n'auraient pas la même géométrie que nous.

Analyse mathématique du texte (proposé par l'irem de Poitiers - GAUD D. - GUICHARD J. - SICRE J-P. - SOUVILLE J. - 1995)

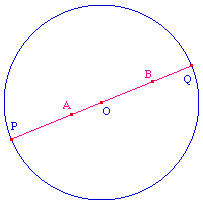
On reprend ce texte d'un point de vue mathématique, dans le cas de la dimention 2. Pour calculer la distance que Poincaré suggère dans ce texte (P-distance dans la suite) entre deux points A et B, on peut commencer par le cas élémentaire où les points A et B dont sur un diamètre du disque.L'hypothèse que propose Poincaré consiste à dire que la distance euclidienne d'un petit segment de P-longueur x est (R²-r²)x/k où k est un coefficient de proportionnalité.

Cas de deux points quelconques

Quand les deux points sont sur un diamètre du cercle, le segment euclidien est bien la P-géodésique qui va de A à B. Mais quand ils ne le sont pas, ce n'est plus le cas, et donc on ne peut intégrer sur le segment euclidien [AB]. Les auteurs du fascicule proposent alors de se ramener au cas précédent par une P-isométrie qui fera de A le centre du cercle.

 non achevé ... ;-(

Menu général