Approximations à l'ordre 2

Développement de Taylor à l'ordre 2 sur l'équation de Riccati

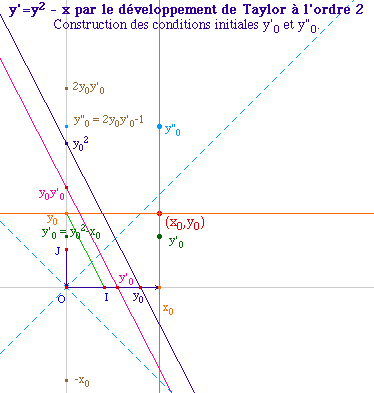
On se propose de passer des conditions (x_n, y_n, y'_n, y"_n) aux conditions (x_n+1, y_n+1, y'_n+1, y"_n+1) pour un pas h = x_n+1 - x_n. Pour cela il convient, au préalable, de déterminer les conditions initiales y'₀ et y"₀.

 

IterT2R1.fig ou IterT2R0.mac (conditions initiales)

Et ensuite de construire le passage d'un point à l'autre. Nous avons voulu privilégier ici la construction géométrique, mais, en utilisant, pour les macros suivantes, les simples calculs dans un repère - comme effectué ci-dessous pour les vérifications - il est probable que les constructions finales seraient moins lourdes en manipulation directe.

IterT2R2.fig ou IterT2R1.mac (en fait y₀ est, comme y'₀ et y"₀, le point "d'abscisse x₀")

 

Itérations successives pour obtenir une approximation en 16 pas

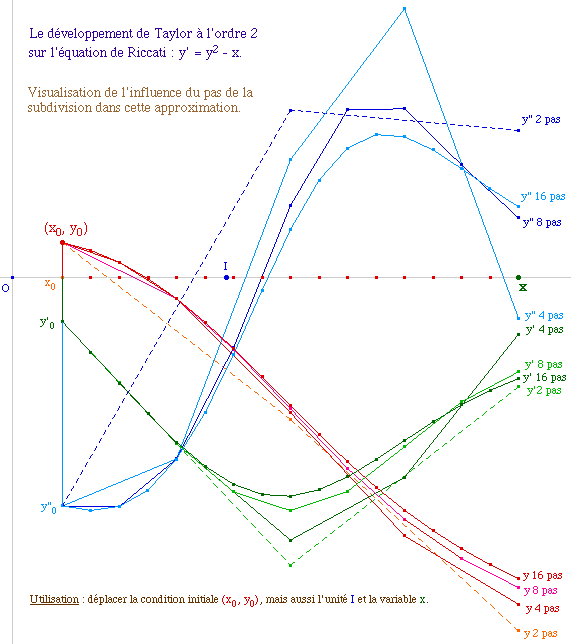
IterT2R3.fig ou IterT2Rh.mac (qui ne renvoie que le dernier point)

Influence du pas de la subdivision

IterT2R4.fig

 

Autre exemple de vérification possible sur la figure précédente

Menu général