Approximation à l'ordre 1 -
Méthode d'Euler
Approximation à l'ordre 1 | Approximations
à l'ordre 2 | L'équation de
Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri]
[Retour EDO] [Retour
"Courbes et équations"] [Menu
général]
|

|
L'idée
générale utilisée dans ces pages sur la
Cabri-intégration des équation
différentielle a été
présentée par Dominique Tournès dans la
version papier d'abraCAdaBRI (n°5
- Sept-Oct 1994) dont un extrait
est rappelé en fin de page : les macros de Cabri nous
permettent d'appliquer une méthode d'approximation
donnée avec un pas suffisament petit pour que la
construction graphique soit pertinente et permettent en
partticulier de proposer des manipulations à des
étudiants orientées vers des activités
de conjecture.
Dans ce dossier, les illustrations sont proposées
sur deux exemples : l'équation de Riccati et une
équation proposée par Euler. Les deux ne sont
pas intégrables à partir des fonctions
élémentaires.
|
Le principe - Première
itération
La méthode d'Euler, sur une
équation d'ordre 1 de type y' = f(x, y), consiste à
prendre localement, en t0+h, pour approximation de
y(t0+h), la valeur y(t0) + hy'(t0).
Autrement dit, localement on approxime la courbe par sa
tangente.
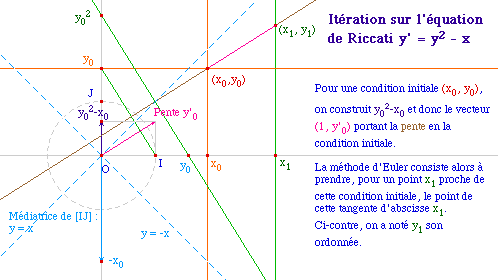
 Iter1R.fig ou Iter1R.mac
Iter1R.fig ou Iter1R.mac
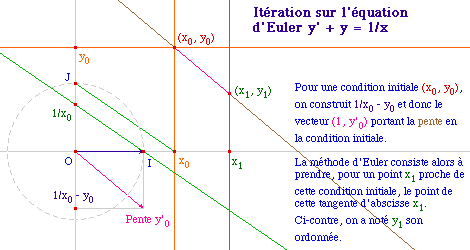
 Iter1E.fig ou Iter1E.mac
Iter1E.fig ou Iter1E.mac
Itérations successives
|
|
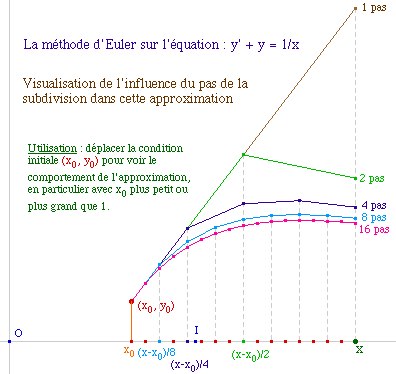
Il est intéressant d'observer la précision
gagnée par l'augmentation du nombre de subdivision
pour aller d'une condition initiale à un un point
donné.
On se limitera dans la suite à 16 pas, le passage
à 32 n'ajouterait pas beaucuop en précision
par rapport au doublement des construction : il faut choisir
un bon compromis entre la précision et la
fluidité de la fiure finale.
Dans utilisation en TP de cette
figure et de la suivante, plusieurs observations peuvent
être faites sur le premier point d'approximation dans
chaque subdivion : par exemple, on passe d'un point à
un autre par une homothétie centrée en la
condition initiale.
 Iter16E.fig ci-contre
Iter16E.fig ci-contre
 Iter16E.mac qui donne
seulement le dernier point de la construction à 16
pas.
Iter16E.mac qui donne
seulement le dernier point de la construction à 16
pas.
|

 Iter16R.fig ou Iter16R.mac
(donnant le point final de la subdivision à 16 pas)
Iter16R.fig ou Iter16R.mac
(donnant le point final de la subdivision à 16 pas)
Utilisation effective : la méthode
d'Euler-Cauchy
Dans les pages suivantes (équation de Riccati et Exemple
d'Euler), nous allons faire le lieu du
point obtenu avec la macro précédente, en 16
subdivisions quand x parcours un segment. Partis de la méthode
d'Euler - lignes polygonales - qui nous a servi à construire
ce point, nous passons à la méthode de Cauchy qui est
de construire non pas une approximation C1 par morceau
mais bien une approximation interne à l'ensemble des
solutions, c'est-à-dire une fonction 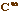 .
.
Voici ce qu'écrivait à ce sujet
Dominique Tournès, historien des
mathématiques, spécialiste des équations
différentielles, lors de sa mise en pratique de la
méthode d'Euler-Cauchy avec Cabri en
1994 :
Pour approcher une courbe intégrale sur tout un
intervalle [x0, x1], la plupart des
traités actuels proposent de construire la ligne polygonale
issue d'un partage de l'intervalle [x0,
x1] en n parties égales et obtiennent ainsi
une fonction continue affine par morceaux, utilisée ensuite
pour approcher la solution en tout point x de l'intervalle.
Ce n'est pourtant pas du tout cette
idée que Cauchy avait à l'esprit en 1824, si
on lit attentivement son Cours d'Analyse de l'Ecole Polytechnique.
Pour Cauchy, la construction précédente ne doit pas
seulement être effectuée pour
l'extrémité x1, mais bien en chaque point
x. La courbe intégrale approchée n'est plus alors
une simple ligne polygonale de classe C1 par morceaux,
mais une courbe parfaitement régulière de même
classe que f [ici de classe 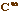 ]. On conçoit que par souci pratique
d'économie, on se contente d'habitude d'un seul calcul
numérique ou d'une seule construction graphique.
Avec Cabri, cette limitation n'a plus de
sens. Prenons x point sur objet de l'axe des abscisses, et
construisons comme ci-dessus la ligne polygonale issue de la
condition initiale pour un partage en 16 de l'intervalle
[x0, x]. Effaçons la ligne polygonale
à l'exception de son extrémité : il nous
reste le point générique de la courbe
intégrale approchée issue de la condition initiale.
Demandons le lieu de ce point quand x décrit l'axe des
abscisses. Nous obtenons la courbe intégrale
approchée imaginée par Cauchy. N'ayons pas peur des
mots :
]. On conçoit que par souci pratique
d'économie, on se contente d'habitude d'un seul calcul
numérique ou d'une seule construction graphique.
Avec Cabri, cette limitation n'a plus de
sens. Prenons x point sur objet de l'axe des abscisses, et
construisons comme ci-dessus la ligne polygonale issue de la
condition initiale pour un partage en 16 de l'intervalle
[x0, x]. Effaçons la ligne polygonale
à l'exception de son extrémité : il nous
reste le point générique de la courbe
intégrale approchée issue de la condition initiale.
Demandons le lieu de ce point quand x décrit l'axe des
abscisses. Nous obtenons la courbe intégrale
approchée imaginée par Cauchy. N'ayons pas peur des
mots :
Cabri permet de retrouver la
vérité historique de la méthode
d'Euler-Cauchy.
L'article de Dominique Tournès
EDOdt.pdf
(70 Ko)
Approximation à l'ordre 1 | Approximations
à l'ordre 2 | L'équation de
Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri]
[Retour EDO] [Retour
"Courbes et équations"]
 Menu général
Menu général




