Approximation à l'ordre 1 | Approximations à l'ordre 2 | L'équation de Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri] [Retour EDO] [Retour "Courbes et équations"] [Menu général]
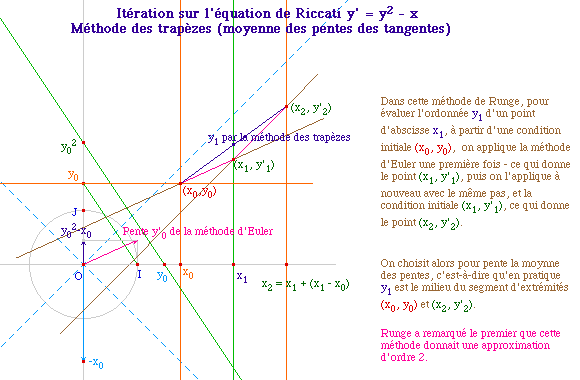
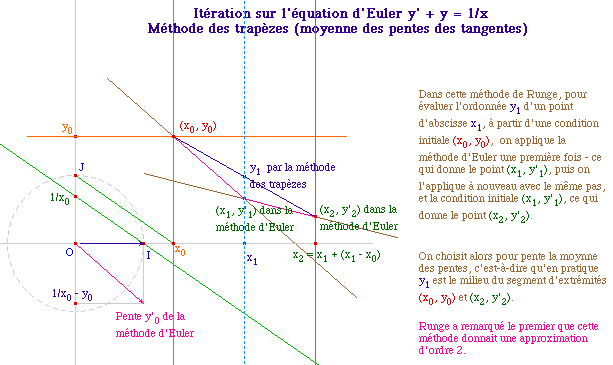
La première méthode a été proposée par Runge ... La seconde est le développement limité à l'ordre 2. Les deux sont naturellement une extension de la méthode d'Euler, qui correspond au DL à l'ordre 1.
Les illustrations sont proposées sur deux exemples : l'équation de Riccati et une équation proposée par Euler. Les deux ne sont pas intégrable à partir des fonctions élémentaires.
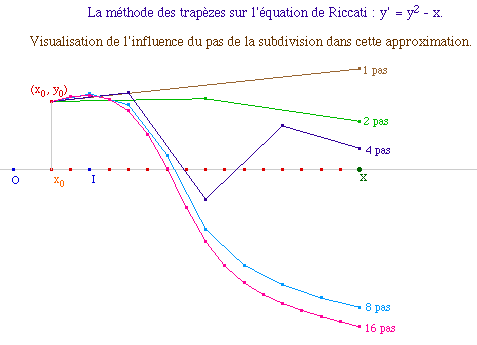
Sur l'exemple de Riccati
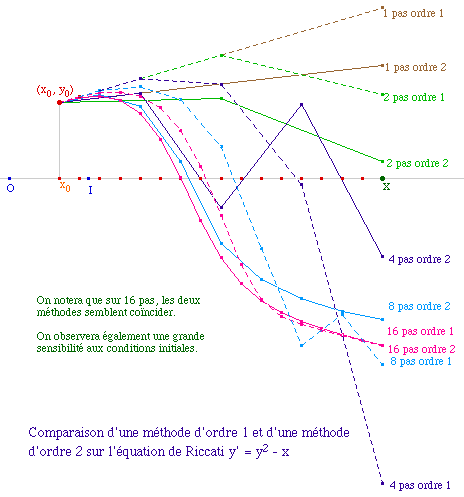
Comparaison avec la méthode d'Euler
Sur l'exemple d'Euler
IterO2E2.fig ou IterO2Eh.mac
Comparaison avec la méthode d'Euler
IterO2E4.fig (la
précédente, dans cette configuration)
Bien entedu, ces figures sont construites pour avoir, par macro, le point courant d'une courbe intégrale que nous obtenons avec Cabri par le lieu de ce point selon la démarche de Cauchy comme rappelé à la page sur l'approximation d'ordre 1.
Exemple de développement de Taylor à l'ordre 2 sur l'équation de Riccati
Approximation à l'ordre 1 | Approximations à l'ordre 2 | L'équation de Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri] [Retour EDO] [Retour "Courbes et équations"]
Menu général
