![]() Euler1.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Euler1.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Approximation à l'ordre 1 | Approximations à l'ordre 2 | L'équation de Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri] [Retour EDO] [Retour "Courbes et équations"] [Menu général]
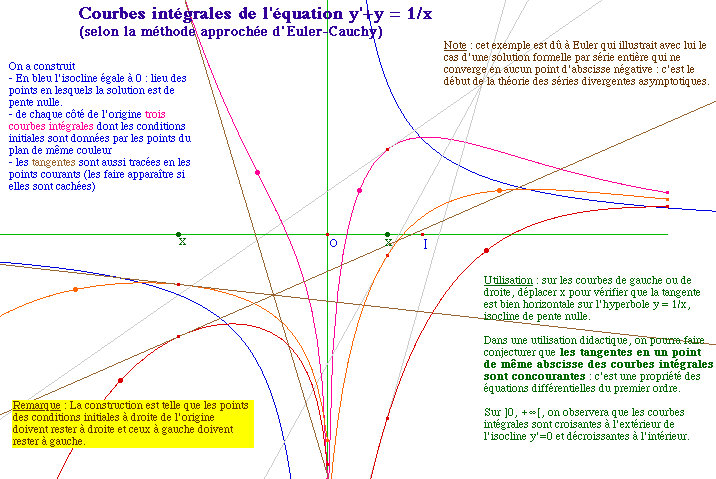
Nous mettons maintenant en oeuvre les macros des pages précédentes. Ces figures permettent, en formation initiale, outre une perception des courbes intégrales en manipulation directe, et des propriétés diverses des isoclines qui peuvent aboutir à des conjectures sur par exemple les ouverts U+ et U-, une autre conjecture sur les tangentes aux courbes intégrales pour une équation différentielle d'ordre 1.

![]() Euler1.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Euler1.fig ou
en manipulation directe dans
le navigateur avec CabriJava
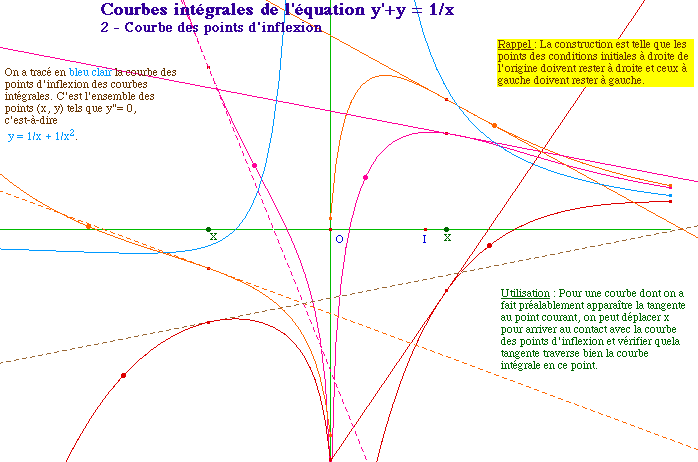
![]() Euler2.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Euler2.fig ou
en manipulation directe dans
le navigateur avec CabriJava
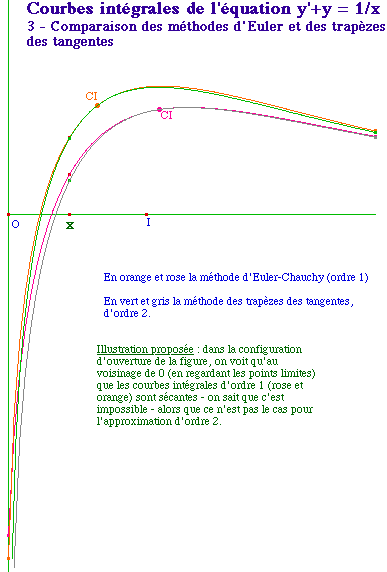
![]() Euler3.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Euler3.fig ou
en manipulation directe dans
le navigateur avec CabriJava
Approximation à l'ordre 1 | Approximations à l'ordre 2 | L'équation de Riccati | Un exemple d'Euler
[Orbites et Trace de Cabri] [Retour EDO] [Retour "Courbes et équations"]