Visualisation du faisceau des
courbes intégrales
d'une EDO par la trace de Cabri
Illustration sur
l'équation de Riccati
Illustration sur l'exemple
d'Euler | Autres exemples | Systèmes
linéaires à coefficients constants
[Retour EDO] [Retour
"Courbes et équations"] [Menu
général]
|

|
Il s'agit ici, non pas de chercher
une approximation d'une courbe intégrale passant par
une condition initiale, mais de brosser rapidement à
l'écran le champ de vecteur associé à
l'équation différentielle. Si le principe est
élémentaire, il n'a été mis en
évidence qu'en 1999, dix ans aprés l'existence
de Cabri. Nous pouvons voir ici une certaine
difficulté que nous avons à penser autrement
l'enseignement avec les outils de géométrie
dynamique dont nous disposons. Le principe exposé ici
a été présenté en octobre 99 par
Jean Marie Laborde lors de la "First Cabri-World Conference"
à Sao Paulo.
|
Le principe
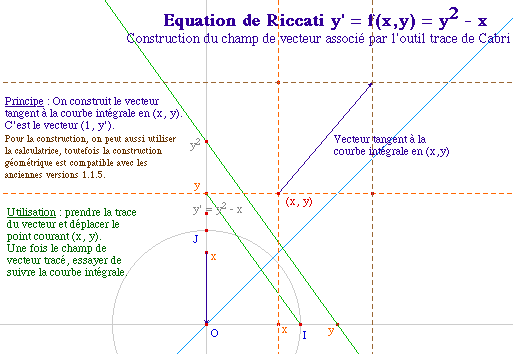
 VectR01.fig ou VectR02.fig
(idem nettoyée pour utilisation)
VectR01.fig ou VectR02.fig
(idem nettoyée pour utilisation)
Application directe

Nous n'avons pas brossé ici la partie x <0 et y <0
car les vecteurs ont une norme trop grande. On commence à voir
le champ de vecteur, mais il y a une amélioration à
apporter, au moins dans le cas de cet exemple.
Utilisation de vecteurs
unitaires
Pour éviter que les vecteurs de trop grande norme masquent
le dessin effectué par la trace, on peut choisir de les
normer, ce qui se fait par l'outil Compas de Cabri, en reportant la
longueur OI sur la demi-droite portée par le vecteur. On a
alors un champ plus homogène, comme ci-dessous :

 VectR03.fig (avec un
vecteur normé)
VectR03.fig (avec un
vecteur normé)
Suivi "kinesthésique" d'une courbe
intégrale
Une fois le champ de vecteur obtenu, on peut ensuite enlever la
trace du vecteur, déplacer le vecteur - ce qui
n'interfère pas sur la trace obtenue - et prendre la trace de
l'origine du vecteur. En essayant alors de suivre la direction du
vecteur, on peut matérialiser l'allure d'une courbe
intégrale. Voici un exemple de ce que l'on peut obtenir
rapidement, en reprenant plusieurs fois l'opération : enlever
la trace du point, déplacer à nouveau le vecteur, et
resélectionner la trace avant de la déplacer.

Illustration sur l'exemple
d'Euler | Autres exemples | Systèmes
linéaires à coefficients constants
[Retour EDO]
[Retour "Courbes et
équations"]
 Menu général
Menu général




