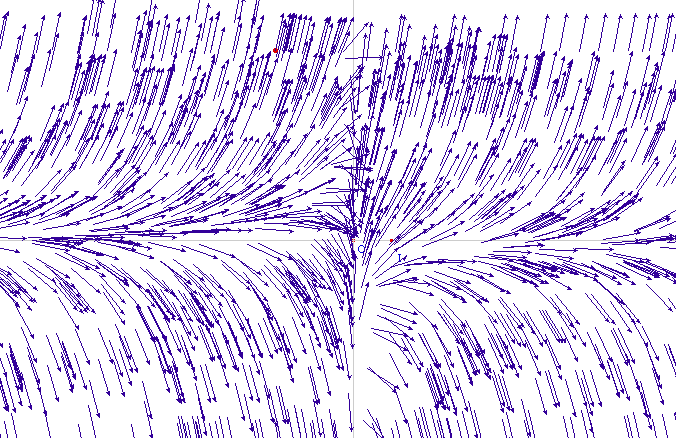
![]() VectE01.fig (vecteurs
normés)
VectE01.fig (vecteurs
normés)
Le procédé a été expliqué à la page précédente sur l'équation de Riccati. Rappelons seulement la manipulation technique que l'on peut proposer en formation :
1 - Balayer (très rapidement) l'écran avec la trace du vecteur.
2 - Décocher la tracer du vecteur
3 - Le déplacer (cela n'altère pas le champ de vecteurs) et penser à positionner correctement la souris ;-)
4 - Activer la trace de l'origine du vecteur
5 - Suivre la direction du vecteur pour matérialiser une courbe intégrale.
6 - Pour recommencer, désactiver la trace du point, et reprendre en 3.
Remarque : quand l'outil trace est sélectionné, les étapes 2, 3, 4 se font sans resélectionner d'outil, directement dans la figure.

![]() VectE01.fig (vecteurs
normés)
VectE01.fig (vecteurs
normés)

En quelques minutes de manipulation, les élèves ont une conception visuelle du champ de vecteur et une conception quasi kinesthésique de la notion de courbes intégrales ...
[Retour EDO] [Retour "Courbes et équations"]