Pour réaliser la construction proposée, on aura besoin de la macro AxeRad.mac qui construit l'axe radical de deux cercles comme proposé ici.

Introduction de l'argumentation

Soient A, B, C, D 4 points et d une droite, on veut construire les coniques passant par les 4 points et tangents à la droite d.

Les coniques passant par 4 points A, B, C et D forment un faisceau linéaire de coniques, chaque conique du faisceau coupe la droite d en deux points, images l'un de l'autre dans une involution définie par ce faisceau (donc ces 4 points) : c'est le théorème de Desargues et Sturm. Les points où la droite d est tangente à une conique du faisceau sont les points doubles de cette involution. Ces points ne sont réels que si l'involution est hyperbolique (les deux couples définissant l'involution ne sont pas séparés) et ne peuvent être construits qu'à l'aide d'intersections de cercles ou de droites et cercles. Autrement dit, le problème admet deux solutions (il y a deux coniques passant par 4 points et tangentes à une droite donnée), mais ces coniques n'existent pas toujours en tant que coniques réelles. Si on a deux couples (M, M') et (N,N') définissant l'involution sur d (on peut choisir M quelconque sur d et M' est la deuxième intersection de la conique passant par les 4 points et M avec d, idem pour N et N'), le problème n'a de solutions réelles que si les cercles de diamètres [MM'] et [NN'] forment un faisceau à points de Poncelet: les points de Poncelet de ce faisceau sont les points où passe une conique définie par les 4 points et tangente à d. Si ces deux cercles se coupent en deux points réels, les points de Poncelet ne sont pas réels et il n'y a aucune conique réelle passant par les 4 points et tangente à la droite d.

Théorème de Desargues - Sturm : voir Deltheil & Caire page 249 (de la seconde partie) - Edition Gabay.

Construction effective.

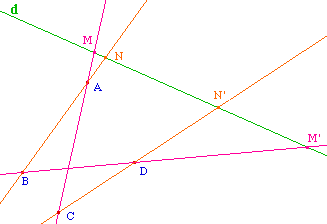On voit tout de suite en se donnant les 4 points de base A,B, C, D et la droite d qu'on peut simplifier la construction de couples de points images l'un de l'autre dans l'involution définie sur d, en choisissant pour coniques du faisceau découpant sur d ces couples de points en involution, les coniques dégénérées du faisceau, par exemple les couples de droites (AC) et (BD), puis (AB) et (CD). Si (AC) coupe d en M, (BD) coupe d en M', (AB) coupe d en N et (CD) coupe d en N'.

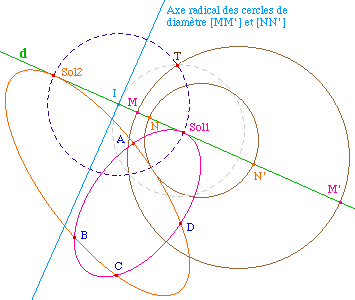
Pour la construction des points limites - de Poncelet - à partir de deux cercles non sécants : Soit I l'intersection de l'axe radical de deux cercles avec la droite des centres (ici la droite d). Le cercle de centre I passant par le point de contact de la tangente issue de I à l'un des cercles - ci-contre passant par T - coupe la droite des centres en les deux points de Poncelet.  Cnk4P1T.fig ou Cnk4P1T.mac Pour cette partie de la construction on peut consulter la première partie du Deltheil & Caire, page 118. PtPoncel.mac qui à partir de d, M, M', N, N', renvoie les deux points doubles de l'involution : les points de Poncelet. (utilisé à la page suivante.

Michel Guillerault rappelle qu'un cas particulier "bien connu" est celui où la tangente est la droite de l'infini : on cherche alors les paraboles passant par 4 points.

Menu général