Cabri-coniques et involution

 2 - Conique connaissant 2 points,
une tangente et son contact et une autre tangente

[1 - Conique par 4 points, une tangente]

[Conf. de Michel Guillerault] [Approche affine] [Retour "Coniques"] [Menu Général]

 

Pour réaliser la construction proposée, on aura besoin de la macro PtPoncel.mac réalisée à la page précédente et de la macro Cnk3P1TC.mac construisant la conique connaisant 3 points, une tangente et son contact comme réalisée ici en application du théorème de Pascal.

 

Présentation

Nous allons utiliser la même démarche que celle proposée par Michel Guillerault à la page précédente, en considérant la tangente en le point donné (C ci-dessous), comme la donné d'un point double et en cherchant les contacts sur l'autre tangente.

 

Construction effective.

 

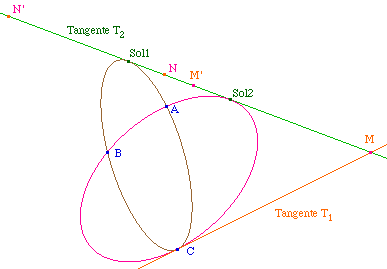
Soient A et B deux points, T1 la tangente dont on connait le point de contact C, et T2 la tangente sur laquelle on cherche les points de contact.

On considère comme première conique dégénérée (en réunion de deux droite) du faisceau linéaire : la tangente T1 et la droite (AB). Elles coupent T2 en M et M'. Puis on considère la seconde conique dégénérée du faisceau : les droites (CA) et (CB). En effet, C étant point de contact, concrètement, on peut l'utiliser deux fois. Cette conique dégénérée coupe T2 en N et N'.

Il suffit d'appliquer la macro PtPoncel.mac à T2, M, M', N et N' pour avoir les deux points de contact solution.

 

C2P1TC1T.fig ou C2P1TC1T.mac

 

 

Les autres cas seront mis en ligne ultérieurement, le lecteur peut les considérer comme des exercices utilisant cette technique,
mais aussi les théorèmes de Pascal, Brianchon, et le cas particulier du théorème de Carnot (céviennes concourantes)

 

 [1 - Conique par 4 points, une tangente]

[Conf. de Michel Guillerault] [Approche affine] [Retour "Coniques"]

 

Menu général