Equivalence entre les définitions

4 - Monofocale vers Bifocale (F, F', 2a)

[1 - Monofocale vers (Foyer, Cercle directeur)] [2 - (Foyer, Cercle directeur) vers Monofocale]
[3 - Lemmes techniques] [5 - Bifocale (F, F', 2a) vers Monofocale] [Retour "Coniques"]

 

Une conique monofocale d'excentricité différente de 1 est bifocale ...

 

Nous avons vu avec la page sur les Axes d'une conique dans la définition monofocale que si l'excentricité est différente de 1, la conique admet un centre de symétrie. Nous avions fait la figure suivante en montrant que si M est sur la conique C(D, F, e) alors M', son symétrique par rapport à la médiatrice des sommets aussi.

Or si on note F' et D' les symétriques de F et D par rapport à ce même axe : M' est un point de la conique C(D', F', e), et par le même argument que ci-dessus M aussi. Autrement dit une conique d'excentricité différente de 1 admet un second foyer et une seconde directrice, symétrique des premiers par rapport à l'axe non focal de la conique, ou encore par rapport à son centre.

Position de l'ellipse par rapport aux directrices

Dans le cas de l'ellipse (e < 1), un point M de la conique est nécessairement du même côté de la directrice D que le foyer associé F : si M est de l'autre côté on a mécessairement MF > MH si H est sa projection orthogonale sur la directrice). De la même façon, M est du même côté que F' de la directrice D'. Cela signifie que :

L'ellipse est entièrement contenue dans la bande délimitée par les deux directrices.

Par ailleurs, remarquons que puisque e<1, F est entre S et S' - et donc F' aussi - et par conséquent K et K' sont extérieur à [SS']. On peut donc écrire KK' = KS + SK'. Par ailleurs, on a également SF + S'F = SS'. Or SF = eKS et S'F = eKS' puisque S et S' sont deux points de la conique de projection K.

On arrive ainsi à la relation : eKK' = SS'.

 

Position de l'hyperbole par rapport aux directrices

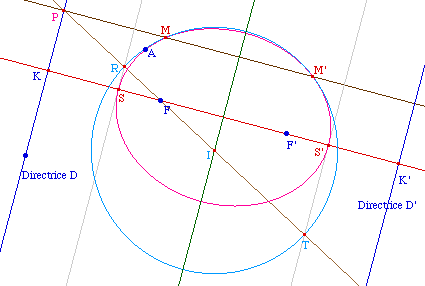
Dans le cas de l'hyperbole (e > 1), la situation est différente :

Puisque e > 1, F est en dehors du segment [SS'] (ligne de niveau), et donc F' aussi par symétrie, alors que pour l'ellipse F était à l'intérieur de [SS'].

Donc F et F' sont à l'extérieur de [SS'], et, puisque KS < SF, K est à l'intérieur de [SS']. De même pour K' : les directrices ont leur projections orthogonales sur l'axe focal à l'intérieur du segment [SS'].

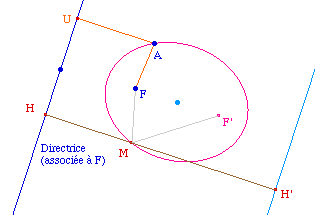
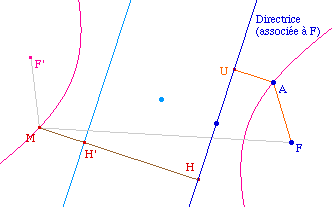
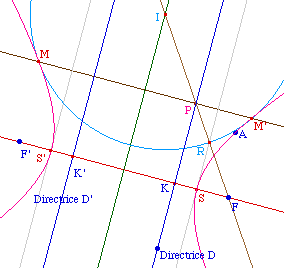
La construction ci-contre des points M et M' de la conique, de projection P sur la directrice prouve alors que la conique est entièrement en dehors de la bande formé par les deux directrice, puisque R est entre P et F.

L'hyperbole est entièrement à l'extérieur de la bande délimitée par les deux directrices.

On peut écrire cette fois-ci que S'F - SF = SS'. Or SF = eKS et S'F = eKS' puisque S et S' sont deux points de la conique de projection K. Comme, cette fois K et K' sont intérieur à [SS'] :

On arrive ainsi à la relation : eKK' = SS'.

Ces positions de la conique par rapport à leurs directrices - justifiée ici de manière uniquement géométrique, va nous permettre de passer facilement d'une définition monofocale à une définition bifocale. La relation entre KK' et SS' permettra une écriture simple des relations trouvées.

On remarquera aussi que ces positions sont aussi des caractérisantions de la différence entre ellipse et hyperbole.

 

... et vérifie les relations sur les rayons vecteurs attendues

 

Cas de l'ellipse (e < 1)

On a vu ci-dessus que la conique est entièrement entre ses directrices. On a donc :

MH + MH' = HH'

de :

MF = e MH
MF' = eMH' et
SS' = eKK' = eHH'
on tire alors :

MF + MF' = SS'.

Cas de l'hyperbole (e > 1)

Cette fois-ci M est à l'extérieur de la bande des deux directrices, et donc si M est un point du même côté que F' de la directrice D', on a :

MF = e MH
MF' = e MH'
SS' = eKK' = eHH'
MF - MF' = e(MH - MH')

soit MF - MF' = eHH'

De même pour un point du même côté que F de la directrice D, avec inversion de signe.
Il en résulte :

|MF - MF'| = SS'

Remarque : si on souhaite retrouver les paramètres des équations réduites, rappelons que e = c/a; les point considérés ont pour coordonnées, dans un repère d'origine le centre de la conique F(0, c), S(0, a) et D a pour équation x = a2/c. (SS' = 2a).

 

[1 - Monofocale vers (Foyer, Cercle directeur)] [2 - (Foyer, Cercle directeur) vers Monofocale]
[3 - Lemmes techniques] [5 - Bifocale (F, F', 2a) vers Monofocale] [Retour "Coniques"]

 

Menu général