Equivalence entre les définitions

2 - Bifocale par Foyer et Cercle Directeur vers Monofocale

[1 - Monofocale vers (Foyer, Cercle directeur)] [3 - Lemmes techniques]
[4 -Monofocale vers Bifocale (F, F', 2a)] [5 - Bifocale (F, F', 2a) vers Monofocale] [Retour "Coniques"]

 

Soit une conique de foyer F et de cercle directeur C', de centre F' et de rayon R. Soit P un point de la conique et C1 le cercle de centre P passant par F. Par définition des coniques par foyer et cercle directeur, ce cercle C1 est tangent à C' en un point M. Les tangentes à C1 en F et en M se coupent en un point T.

 

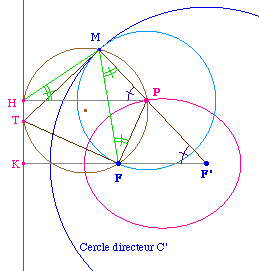
Expérimentation : le lieu de T est une droite perpendiculaire à l'axe focale (FF').

Soit donc d la perpendiculaire à (FF') passant par T.

d est indépendante de P car, par TF = TM, T est, par définition, l'axe radical du cercle C' - de centre F' - et du cercle-point F.

BiFCMono.fig

Preuve

En notant H la projection orthogonale de P sur d, il y a, comme dans le sens direct, cocyclicité des points P, F, T, H et M. On a les mêmes égalités d'angles, les triangles PMF et F'FM sont semblables, d'où les égalités :

PM/PH = FF'/F'M, soit PF/PH = FF'/R = e (avec e différent de 1 car FF' est différent de R).

Ainsi d est la directrice de la conique de départ, associée à F et e = FF'/R.

 

 

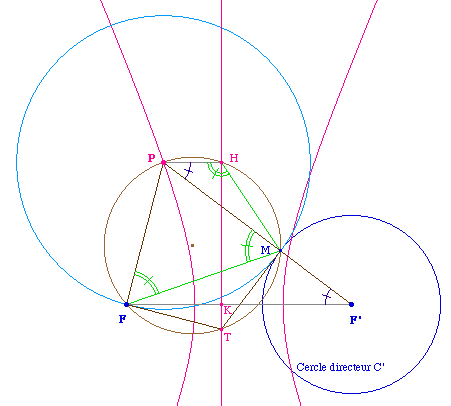
Illustration dans le cas de l'hyperbole

 

 

[1 - Monofocale vers (Foyer, Cercle directeur)] [3 - Lemmes techniques]
[4 -Monofocale vers Bifocale (F, F', 2a)] [5 - Bifocale (F, F', 2a) vers Monofocale] [Retour "Coniques"]

   

 

Menu général