|
|
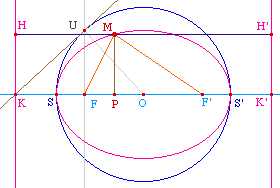
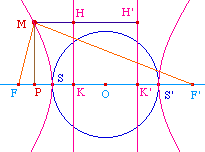
S et S' sont donnés, et on note O leur milieu. Soient F et F' deux points du segment [SS'], symétriques par rapport à O (F appartient au segment [OS]). Ce qui précède permet d'affirmer qu'il existe un unique point K de (SS') tel que le cercle de diamètre [SS'] soit une ligne de niveau MF/MK = e. K est extérieur au cercle, puisque sur une tangente. Ce même cercle, par symétrie par rapport à la médiatrice de [SS'], est aussi la ligne de niveau MF'/MK' = e, où K' est le symérique de K par rapport à O.On suppose donc que MF + MF' = SS' et on veut montrer que M appartient à la conique de foyer F de directrice la perpendiculaire à (FF') passant par K et d'excentricité OF/OS. |