|
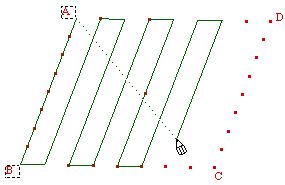
L'idée est simple : on se
donne un repère (O, I, J, K) on calcule les
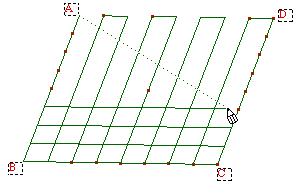
coordonnées du point M, sur objet de la grille dans
(O, I, J), on applique une fonction à ces
coordonnées, que l'on reporte en côte par un
point N, après conversion dans le repère (O,
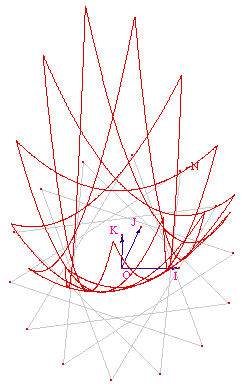
K). Le lieu de N quand M parcourt la grille donne l'image de
cette grille par la fonction.
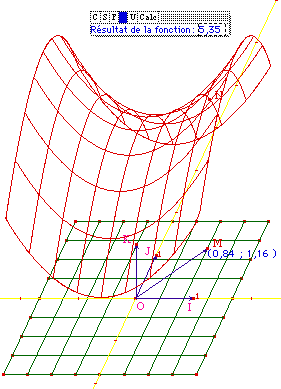
De plus, il suffit de changer la fonction dans Calc pour
faire un autre tracé (ici le tracé est celui
de f(a, b) = 6 + a2 - b2).
Sur cette figure, le plan (O, I,
K) est le plan frontal, les unités sont modifiables
par les points I, J, K. les variables a et b de la fonction
sont les coordonnées de M dans le repère (O,
I, J). Pour un autre tracé, seul ce calcul est
à modifier.
|