|
|
|
|
"Traduire d'anciens savoirs dans de nouvelles technologies intellectuelles revient à produire de nouveaux savoirs. L'illusion consiste à croire qu'il y aurait des "connaissances" ou des "informations" stables qui pourraient changer de support, être représentées autrement ou simplement voyager tout en gardant leur identité. Illusion car ce dont s'occupent les théories de la connaissance : savoir, information et signification sont précisément des effets de supports, de connexions, de proximités, d'interfaces." Pierre Lévy |
Il est intéressant d'observer que dans le passé, le changement de transfert de support a engendrer de nombreux bouleversements dans la pratique des mathématiques savantes de l'époque et dans l'enseignement des mathématiques en général. Sans entrer dans des détails trop fastidieux, signalons toutefois deux exemples significatifs, le premier en Chine, le second en Europe.
Les baguettes à calculer, que l'on dispose sur une planche de bois quadrillée (une sorte d'échiquier) apparaissent vers le II° siècle avant JC et sont d'un usage courant jusqu'au XIII° siècle après JC. Ce support à deux dimensions permet le développement de calculs complexes : Ainsi, on trouve la méthode du pivot de Gauss pour la résolution de systèmes d'équations linéaires 3x3 dès le I° siècle avant JC!
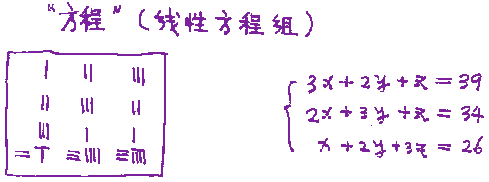
Cette disposition permet bien sûr l'écriture
d'un système d'équations linéaires,
mais aussi sa résolution comme le montre la figure
ci-contre. En multipliant et soustrayant les colonnes, on
obtient de proche en proche un système triangulaire
qu'on sait résoudre facilement.
Bien que, pour expliquer la méthode
utilisée, on ait dû "écrire" les
différentes étapes de la résolution du
système précédent, il faut garder
à l'esprit que cette résolution s'effectuait
uniquement en manipulant les baguettes sur la surface
à calculer.
On peut ainsi admirer les prouesses de Liu Hui qui, au
IIIe siècle, en manipulant seulement des baguettes
à calculer, était parvenu à approcher
le nombre ¼ avec six décimales exactes.
Ci-contre et ci-dessous sont des extraits d'un
passionnant article
Nombres, outils de calcul et
expressions mathématiques en Chine ancienne
Par LIU Dun - Directeur de
l'Institut d'histoire des sciences de Pékin
Article disponible (600 Ko en .pdf) dans les
actes du colloque d'histoire des maths de novembre 97
organisé par Dominique
Tournès à l'IUFM
de La Réunion

On trouve également des équations polynomiales à une ou plusieurs inconnues : jusqu'à 4 inconnues, représentées sur la table à calculer par les 4 directions cardinales.
Zhu Shijie dans son Miroir de jade des quatre inconnues (1303) traite d'équations polynomiales à quatre inconnues (exemple ci-dessous). Au centre on place le terme constant (ici 0, représenté par le caractère tai), puis, en partant du centre, les coefficients des quatre inconnues, suivant leurs puissances croissantes, respectivement - pour ci-dessous x, y, z, et t - dans les directions sud, ouest, nord et est ; les termes rectangles sont alors placés naturellement dans l'un des quadrants, à l'intersection de la ligne et de la colonne correspondant aux puissances des deux inconnues.
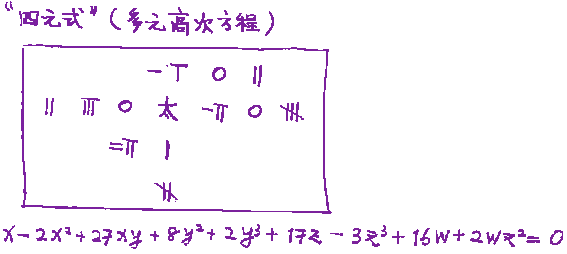
Lorsque le boulier apparaît, vers le XIII° ou XIV° siècle, il se révèle beaucoup plus pratique pour les calculs courants - les 4 opérations - des commerçants, artisans, etc. Il l'emporte face aux baguettes à calcul. Mais ce changement de support entraîne une régression de la pratique mathématique de haut niveau : le boulier, instrument linéaire, ne permet pas de calculer simultanément sur plusieurs nombres disposés en tableau.
Les calculateurs avaient hérité de l'époque romaine la pratique des calculs sur l'abaque à jetons (on déplace des jetons sur une planche divisée en colonnes). En effet, les chiffres romains ne permettent aucune sorte de calcul : ils servent seulement à écrire les nombres, en aucun cas à opérer sur eux. Vers le XII° siècle, au retour des croisades et
à la suite de contacts avec les arabes d'Espagne et d'Afrique du Nord, la technique du calcul indien avec les chiffres arabes et le zéro est ramenée d'Orient. Les savants (un des premiers étant Fibonacci) adoptent avec enthousiasme le nouveau calcul écrit qui va permettre l'envol des mathématiques en Occident. Par contre, les commerçants, comptables, artisans, etc. continuent à utiliser l'abaque à jetons. La querelle est vive entre les abaquistes (tenants de l'abaque) et les algoristes (tenants du calcul écrit). En France, elle se prolonge jusqu'à la Révolution qui interdit officiellement et définitivement l'usage de l'abaque dans les écoles et les administrations.
Nous sommes sans doute en train de vivre un changement de support comparable aux deux précédents : le calcul indien écrit est en voie d'être remplacé par le calcul sur calculatrice. À un plus haut niveau, le calcul algébrique papier-crayon est remplacé par les logiciels de calcul symbolique, et les figures de géométrie papier-crayon-règle-compas par les logiciels de géométrie dynamique. Cette mutation semble s'accompagner de changements profonds au niveau de la recherche mathématique : revalorisation des mathématiques appliquées, création de véritables mathématiques expérimentales (on commence à voir publier dans les revues mathématiques des articles où se mêlent des démonstrations incomplètes et des conjectures appuyées par des calculs gigantesques sur des exemples), recul des grandes constructions abstraites de la première moitié du XX° siècle (algèbre homologique, entre autres) qui étaient d'une certaine façon la conséquence du fait qu'on avait atteint les limites du calcul papier-crayon et qu'on se réfugiait dans des spéculations non constructives sur des objets de plus en plus sophistiqués.
Signalons également le suicide significatif du Grand Nicolas en 1998 ... pour ses cinquante ans.
|
|
"Il nous semble tout aussi important de mettre à distance des représentations qui nous conduisent à penser la légitimité en termes d'adéquation aux valeurs et normes héritées des environnements usuels." Michèle Artigue |
Les élèves évoluent désormais dans un environnement culturel qui n'est plus dominé par les valeurs engendrées par l'écrit - comme la trace, la séquence, les notions de vérité, et donc de théorie (référentes) et d'objectivité - mais par celles de l'information et de la communication où les valeurs émergeantes sont de l'ordre de l'immédiateté (le temps réel), la simulation, l'efficacité, ou la pertinence locale. Ce changement de valeurs culturelles provoquent de nouveaux rapports aux savoirs et à leurs apprentissages.
Voici un extrait d'un tableau d'analyse proposé par Pierre Lévy ("Les technologies de l'intelligence" - Point Science - 1993)
|
|
l'oralité primaire |
l'écriture |
informatico-médiatique |
|
Cercles |
Lignes |
Segments, points |
|
- Horizon de l'éternel retour. - Devenir sans repère ni trace. |
- Histoire, sous l'horizon d'un accomplissement. - Traces, accumulation. |
- Vitesse pure sans horizon. - Pluralité des devenirs immédiats. (La dynamique fondamentale de ce pôle reste partiellement indéterminée) |
|
- Inscription dans une continuité immémoriale.
- Immédiateté.
|
- Délais, actes de différer. - Inscription dans la durée, avec tous les risques que cela implique.
|
- Temps réel. - L'immédiateté a étendu son champ d'action et de rétro-action à la mesure du réseau informatico-médiatique. |
|
- Récit. - Rite. |
- Théorie (explication, fondation, exposé systématique) - Interprétation
|
- Modélisation opérationnelle ou prévisionnelle. - Simulation. |
|
- Permanence ou conservation. - Signification (et sa dimension émotionnelle). |
Vérité selon les modalités de - la critique, - l'objectivité, - l'universalité. |
- Efficacité. - Pertinence locale. - Changement, nouveauté. |
Compléments
sur ce thème
Site "maths" - IUFM de La Réunion
On peut en particulier s'interroger sur cette capacité nouvelle qu'ont parfois les lycéens à inverser le rôle que la culture de l'écrit accorde respectivement au processus d'acquisition des connaissance et au savoir : chacun peut en effet observer que le savoir ou savoir faire à acquérir (par contrat avec une institution d'éducation ou de formation) dans certains cas devient un moyen d'enrichir sa propre approche des processus d'apprentissage. Les savoirs ou savoir faire qui, il y a encore peu, assuraient une stabilité professionnelle, sont désormais trop volatils (perçus comme relevant simplement d'une pertinence locale) et, s'ils sont incontournables pour être au présent, sont surtout un moyen de forger son propre "savoir-devenir" .
Or ceci n'est possible que par une objectivation du processus d'acquisition des connaissances. Or c'est justement une des questions soulevées dans l'utilisation d'un logiciel de géométrie dynamique comme Cabri-géomètre, ou de figures dynamiques sur le Web comme avec CabriJava : une pratique régulière favorise cette objectivation. Dans ce cas la motivation des utilisateurs est critériée par le processus d'apprentissage lui-même, en particulier par ses propres capacités de simulation.
Ainsi serait-il possible que Cabri et CabriJava, de par leur ouverture à une culture de simulation, soient parfois détourné des modes de fonctionnement autour desquels ils ont pu être conçus vers d'autres qui autoriseraient dans un cadre strictement scolaire l'exercice de l'apprentissage comme objectif premier d'un savoir faire (encore) à acquérir ?
|
 Retour sur
"abra-Java"
Retour sur
"abra-Java" |