|
|
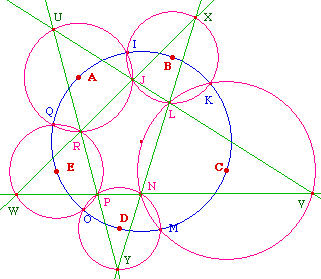
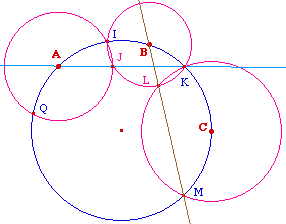
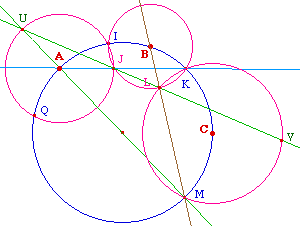
À partir d'un cercle C (gamma), on construit 5 cercles Ci,dont les centres sont sur C, et tel que Ci et Ci+1 soient aussi sécants en un point de C, ainsi que C5 et C1 : ainsi, ci-contre C1 est de centre A passant par I, C2 de centre B passant aussi par I, A, B et I étant sur G, etc. On notera dans la suite un cercle par son centre : CA ... etc.(JL) recoupe CA et CC en U et V. (LM) recoupe CB et CD en X et Y.Théorème de Miquel :Alors (PN) passe par V, (RP) par U et Y. De même si (PN) coupe CE en W alors (RJ) passe par X et W : on a ainsi un petangone (irrégulier) UVWXY. |