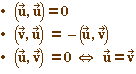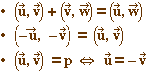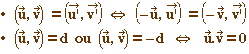Résumé sur les
angles
1 - Angles orientés de
vecteurs du plan
[Synthèse sur les angles
orientés] [2-Mesure des
angles orientés du plan] [3-Angles
orientés de droites vectorielles]
[4-Angles non orientés dans le
plan ou dans l'espace] [5-Angles
dans un espace affine euclidien]
[Retour "Angles /
Cocyclicité"] [Retour
Géométrie 2D]
E désigne un plan vectoriel
euclidien et 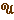 l'ensemble des vecteurs unitaires (de norme 1) de E.
l'ensemble des vecteurs unitaires (de norme 1) de E.
Angles orientés de deux vecteurs
unitaires
Propriété des rotations : Soient  et
et 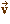 deux vecteurs unitaires, il existe une unique rotation r telle que
r(
deux vecteurs unitaires, il existe une unique rotation r telle que
r( ) =
) =
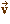 .
.
Conséquence : 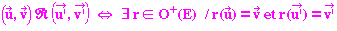 est une relation d'équivalence dans l'ensemble
est une relation d'équivalence dans l'ensemble 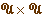 .
.
Définition : L'angle
orienté du couple 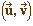 est la classe d'équivalence de
est la classe d'équivalence de 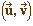 pour la relation
pour la relation 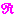 ,
notée encore
,
notée encore 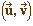 .
On note
.
On note 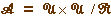 l'ensemble des angles orientés.
l'ensemble des angles orientés.
Définition : L'angle d'une
rotation r est l'angle 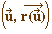 pour
un vecteur unitaire
pour
un vecteur unitaire  quelconque.
On notera ra la rotation d'angle a.
quelconque.
On notera ra la rotation d'angle a.
Angles orientés de deux vecteurs non
nuls ou de deux demi-droites
Soient  et
et 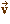 deux vecteurs non nuls, d = R+
deux vecteurs non nuls, d = R+  et d'= R+
et d'= R+ 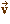 les demi-droites vectorielles qu'ils engendrent, on définit
les angles orientés de ces vecteurs ou de ces demi-droites par
:
les demi-droites vectorielles qu'ils engendrent, on définit
les angles orientés de ces vecteurs ou de ces demi-droites par
:
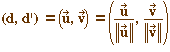
Transport de structure sur
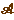
L'application 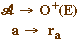 qui à un angle a associe l'unique
rotation ra d'angle
a est une bijection.
qui à un angle a associe l'unique
rotation ra d'angle
a est une bijection.
(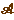 ,
+) est muni d'une structure de groupe par transfert de
structure :
,
+) est muni d'une structure de groupe par transfert de
structure :
a+b est l'angle tel que ra+b = ra o
rb.
-a est l'angle tel que r-a =
ra-1.
0 est l'angle tel que r0 = IdE.
Théorème
(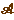 ,
+) est un groupe commutatif, isomorphe à
(O+(E), o)
,
+) est un groupe commutatif, isomorphe à
(O+(E), o)
Vocabulaire
angle plat p = angle de la rotation
- IdE.
angles droits d et -d = angles des
deux rotations ayant pour matrice 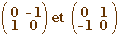 dans un base orthonormée.
dans un base orthonormée.
Propriétés des angles
orientés de vecteurs unitaires
Les rotations conservent les angles orientés, les
réflexions les changent en leurs opposés.
[Synthèse sur les angles
orientés] [2-Mesure des
angles orientés du plan] [3-Angles
orientés de droites vectorielles]
[4-Angles non orientés dans le
plan ou dans l'espace] [5-Angles
dans un espace affine euclidien]
[Retour "Angles /
Cocyclicité"] [Retour
Géométrie 2D]
 Menu
général
Menu
général