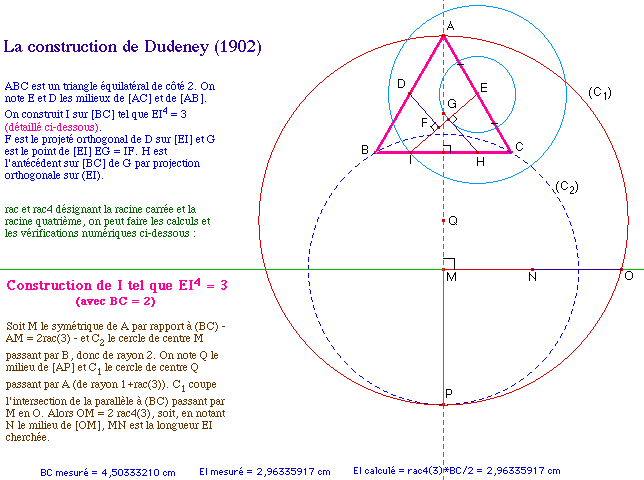
La construction

On considère un triangle équilatéral de côté 2. Si un carré est de même aire, son côté c est tel que c⁴ = 3 (le côté est la racine quatrième de 3).

  DudOK.fig

Une construction approchée

On rencontre parfois, dans certains ouvrages, une construction de la racine quatrième de 3 (côté du carré de même aire que le triangle de côté 2) mentionnée comme exacte alors qu'elle n'est qu'une approximation. On a toutefois la transformation du triangle équilatéral en un rectangle :

 

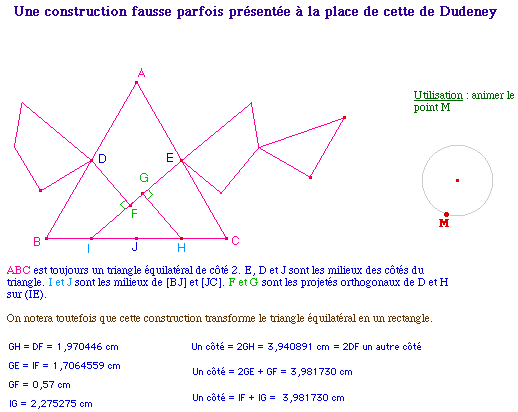
  DudFaux.fig (on y mesure une erreur de 1%)

 

 Une superbe application en CabriJava de Eric Hakenholz

Des calculs élémentaires donnent (c étant le côté du carré, comme ci-dessus)

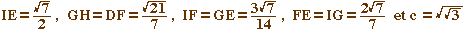
Si ce découpage permettait d'obtenir un carré, d'une manière ou d'une autre, il existerait une Q-combinaison linéaire de 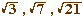de somme c. Alors il existe x, y, z, t, rationnels tels que : 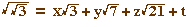. En élevant deux fois au carré, on arrive, par exemple, à l'irrationnalité de .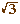

Il est donc impossible de réaliser un carré avec les 4 pièces de ce puzzle. On otera que cela prouve qu'aucun arrangement de ces 4 pièces n'est un carré. On peut cependant obtenir un rectangle dont la longueur et la largeur sont très proches de c comme observé dans la figure ci-dessus.

Contact avec l'auteur des figures Cabri : Alain Rousseau

Menu général