Soit deux droites d et d', parallèles, et deux points distincts points A et B n'appartenant pas à ces droites. On demande de construire les coniques de passant par A et B, et ayant d et d' comme directrices.

Pour construire les coniques on aura besoin de :

Charger la macro Conique par F, D, A qui construit une conique par foyer, directrice et un point. Cette macro est aussi contenue dans la figure ci-dessous.

L'idée générale est trés simple, elle est basée sur les cercles d'Appolonius, c'est à dire sur les lignes de niveau de type MA/MB = k. Deux approches sont possibles, et on va voir que l'une est plus efficace que l'autre ...

Première construction

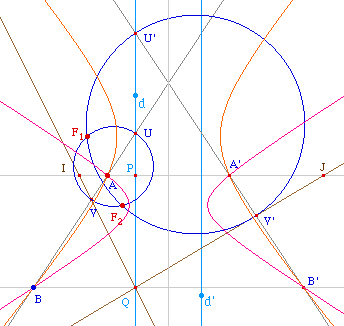
Cas ou les points sont à l'extérieur de la bande formé par les directrices : il y a deux deux hyperboles solution.

Si on connaît deux points A et B et une directrice d, il est facile de construire le lieu des foyers associés à la droite d, des coniques passant par A et B de directrice cette droite. Cette situation a déjà été explorée en détail dans cette page. C'est ce qui est fait ci-dessous : la droite (AB) coupe la directrice d en U, si on note P et Q les projections orthogonales de A et B sur d, et I le symétrique de P par rapport à A, la droite (IQ) coupe (AB) en V tel que le cercle de diamètre [UV] est le lieu des points F tels que AF/BF = AP/BQ soit encore AF/AP = BF/BQ ce qui correspond à l'excentricité de la conique cherchée. Connaissant maintenant une seconde directrice d', il est facile de construire deux autres points A' et B' de la conique. Le lieu des foyers - toujours associés à la directrice d - des coniques passant par A' et B' est le cercle de diamètre [U'V'] où U' est l'intersection de (A'B') avec d et V' l'intersection de (A'B') avec (QJ), J étant le symétrique de P par rapport à A' puisque A' et B' ont eux aussi, respectivement P et Q comme projeté orthogonal sur d.

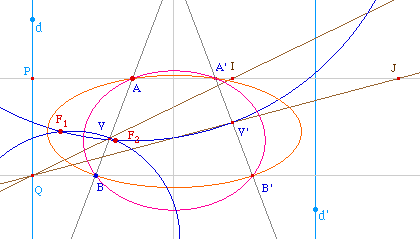
Cas ou les points sont à l'extérieur de la bande formé par les directrices : il y a deux deux ellipses solution.

Si ces deux cercles se coupent, les intersections - F1 et F2 sur l'illustration - sont les foyers solutions. Sinon, il n'y a pas de solution. C'est par exemple le cas si l'un des points est à l'intérieur de la bande délimitée par les deux directrices et l'autre pas.On en déduit que dans ce cas, les deux coniques solutions sont de même type. La figure SolC03a.fig ci-contre. Il est clair toutefois que cette construction est prise en défaut quand la droite (AB) est paralléle à la directrice d, alors qu'il existe toujours, en général, deux solutions. Dans ce cas, on pourrait s'en sortir en appliquant la macro non pas aux points A et B, mais aux points A et B', ce qui convient. Mais cette astuce est inutile si on traite la question d'une autre façon. C'est ce que nous allons faire maintenant.

Pour éventuellement comparer les deux constructions, on peut

Charger la macro Cnk2D2p1.mac correspondant à la figure ci-dessus (suffixe "NPD" pour rappeler que (AB) doit être Non Parallèle à la Directrice).

Seconde construction

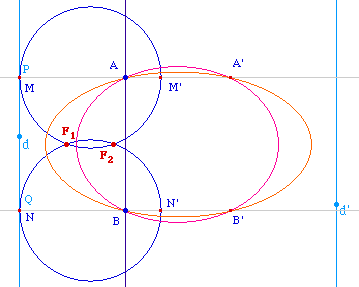
Au lieu de construire les cercles d'Appolonius relatifs aux couples (A, B) puis (A', B'), on peut construire les cercles relatifs aux couples (A, A') puis (B, B'). En effet, le lieu des foyers F associés à la directrice d doit vérifier AF/AP = A'F/A'P (=e) puisque la conique passe par A et A', donc F est sur le cercle d'Appolonius FA/FA' = PA/PA' de diamètre [MM']. En pratique, puisque A, P et A' sont alignés , M et M' sont les centres d'homothétie des cercles de centre A et A' passant par P. Le cercle de diamètre [MM'] est le premier lieu du foyer F associé à d. Remarque : On prendra soin de construire M et M' car, pour des questions d'orientation dans Cabri P n'est pas le point M', mais l'un des deux points M ou M'. On vérifiera par exemple que M est en P quand A est entre les droites d et d'. On fait de même avec les cercles de centre B et B' passant par Q, les foyer est aussi sur l'autre cercle de diamètre [NN'] construits comme ci-dessus (avec la même remarque). Les deux cercles se coupent en deux foyers F1 et F2. On applique la macro conique de la première construction.

 

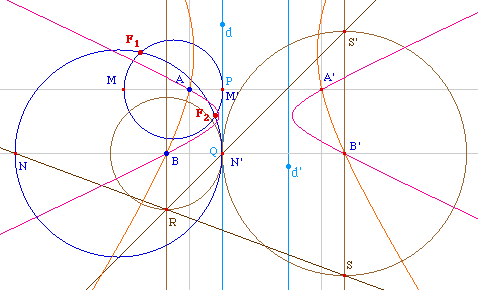
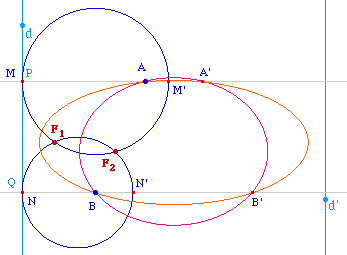
	Lancer la figure SolC03b.fig ci-dessus ou la même épurée : SolC03c.fig comme à l'illustration ci-contre.   On observera en particulier l'inversion des points M et M' en P et N et N' en Q quand A et B sont à l'intérieur des directrices.
	On vérifiera que cette construction est naturellement opérante quand la droite (AB) est parallèle à la directrice. Dans ce cas, MM' = NN', et les coniques ont nécessairement le même axe focal. C'est même trivialement une CNS. Remarque : Dans cette seconde méthode, il est clair que, par construction, les deux cercles lieux de F sont simultanément à l'extérieur ou à l'intérieur de la bande formée par les deux directrices. Ceci justifie que l'on ait simultanément deux ellipses ou deux hyperboles. Charger la macro Cnk2D2p2.mac correspondant à la figure ci-contre (suffixe "G" pour rappeler que cette macro fonctionne dans tous les cas).
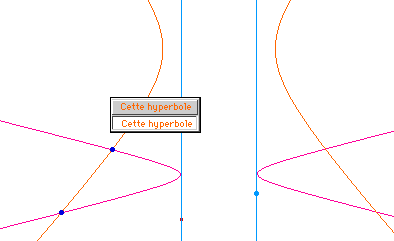
	On peut, à une figure, appliquer les deux macros pour vérifier qu'elles donnent bien les mêmes coniques ...

Retour à la page d'exercices

Menu général