On se propose de construire la section d'un double cône inverse par un plan, de manière que l'on puisse modifier le plan de la section et changer le point de vue par une rotation horizontale.
1. Construction du cône en perspective
|
|
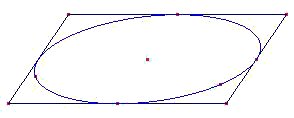
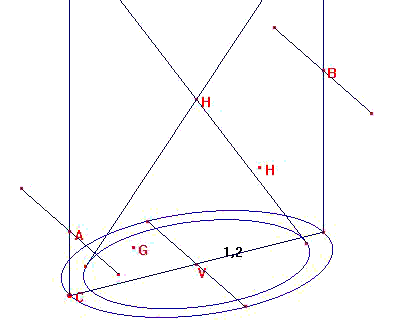
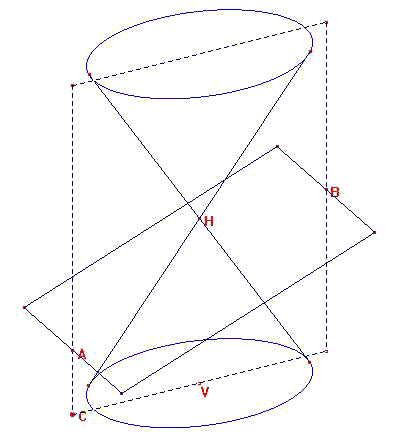
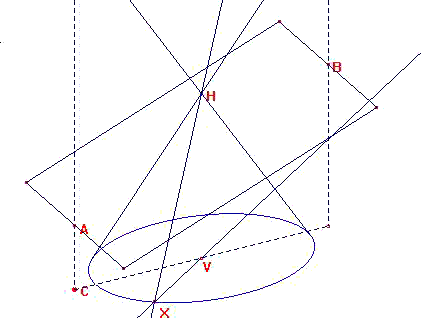
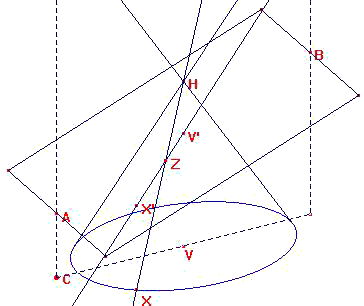
On désire construire un cône circulaire droit en perspective, donc la base du cône sera un cercle en perspective, c'est a dire une ellipse. On commence par définir le plan de la base en construisant un parallélogramme. |
|
|
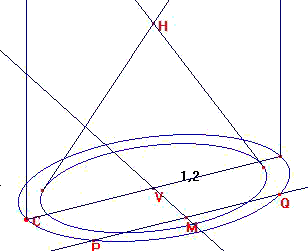
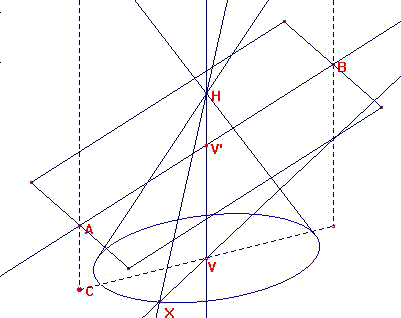
Puis on applique la macro
|
|
|
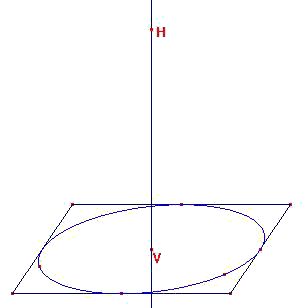
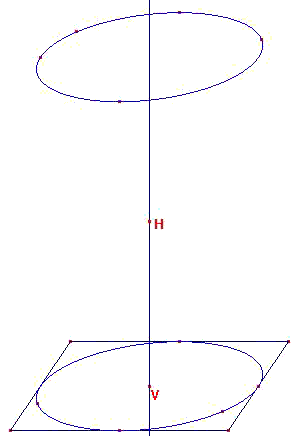
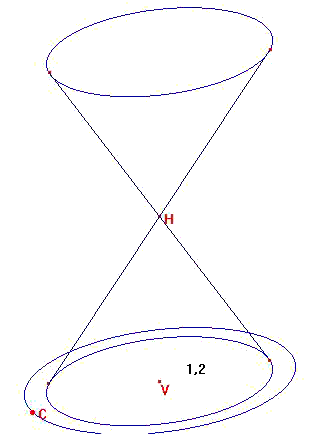
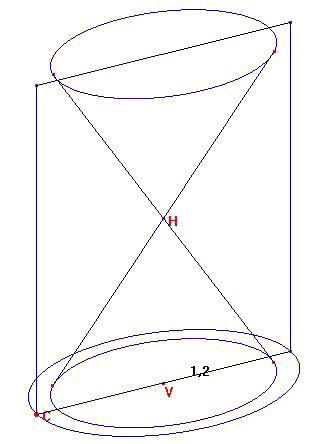
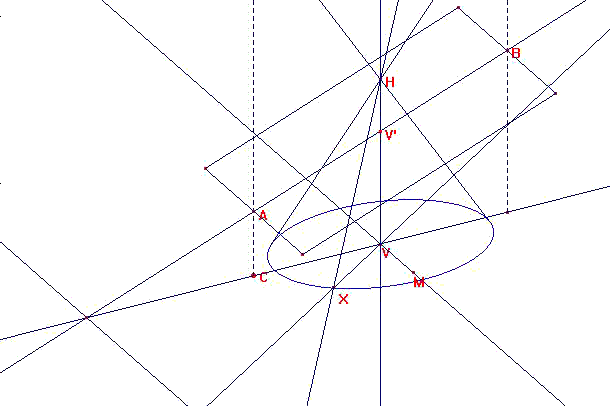
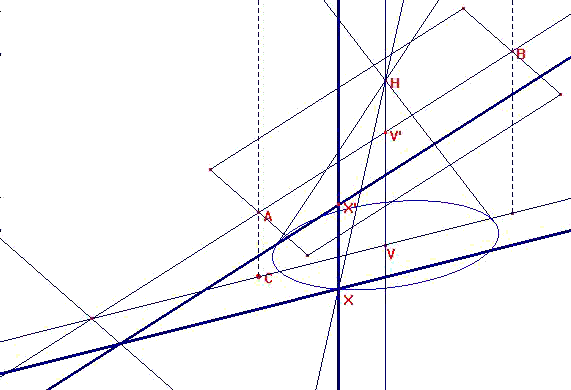
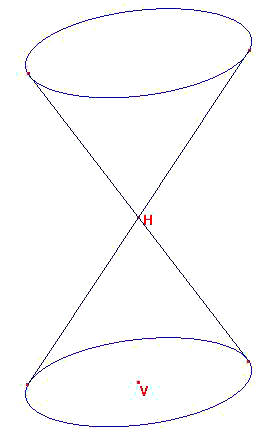
On définit après le sommet du cône en construisant un point H sur la droite verticale passant par V,
|
|
|
 |
Il ne reste qu'a choisir deux points sur une des bases et leurs symétriques sur l'autre base, et tracer les génératrices du cône.
2. Construction du plan de section
|
|
D'abord on va définir un point qui tourne autour de la base, pour contrôler ainsi les différents points de vue horizontaux. |
|
|
Avec le symétrique de C par rapport au centre, on peut construire un segment diamètre de l'ellipse. Et avec le symétrique de ce segment par rapport au point H, on peut construire un parallélogramme représentant le plan qui contient la hauteur.
Afin d'assurer l'orthogonalité du deuxième plan avec celui qu'on vient de construire, il faut trouver le diamètre conjugué du diamètre contenant C. On utilise la propriété de toute conique suivant laquelle les cordes parallèles ont leurs milieux sur un diamètre. Ainsi, si se construit une droite parallèle a CV par un point P de l'ellipse, elle coupera l'ellipse en deuxième point Q, et le milieu M de [PQ] est sur le diamètre conjugue de [CV]. Il ne reste qu'a tracer la droite (VM), qui est perpendiculaire à [CV] dans l'espace, est sur elle construire le diamètre conjugué. |
|
|
En plaçant deux points A et B sur le parallélogramme représentant le plan verticale, on peut contrôler l'inclination du plan de section. On construit G, milieu de [VA] et H milieu de [VB], et par symétrie on transforme le diamètre conjugue de [CV] sur A et B respectivement. |
|
|
Il ne reste qu'a tracer le parallélogramme correspondant au plan de la section. |
|
|
On a maintenant le double cône et le plan de la section, avec la possibilité de changer le point de vue horizontale en déplaçant C, et l'inclination du plan de section en déplaçant A et B. Il reste encore la partie cruciale de la construction, celle de la section proprement dite. |
3. Construction de la section
|
|
Pour obtenir la section désirée, il suffit de prendre une génératrice du cône et trouver l'intersection (dans l'espace) de cette droite et le plan de section. Mais comment trouver cette intersection dans le plan de projection? On doit construire une droite qui soit sur le plan de section, et qui coupe la génératrice. Prenons donc un point X sur le cercle (ellipse) de la base. Ce point définit un diamètre du cercle, c'est a dire une droite qui passe par le centre V. Aussi, la droite (XH) est une génératrice du cône. On peut construire facilement la projection du point V sur le plan de section. |
|
|
Si l'on arrive a projeter sur ce plan le point X, on aurait aussi la projection du diamètre passant par X, et de cette manière la droite cherchée. On doit donc construire la projection du plan horizontale sur le plan de section, ce qui revient a construire une homologie sur le plan de l'écran. Cette homologie transforme V en V' et laisse invariante la droite qui représente l'intersection du plan horizontale et le plan de section. Commençons par construire cette droite. Pour ce faire, on prolonge les segments [AB] et [CV], et on construit la parallèle à (VM) par l'intersection de ces deux droites. |
 |
On occulte les droites (VM) et (XV) afin de faire plus claire la construction. Puis, en traçant des parallèles à (CV), (AB), et (VH) on trouve le point X' projeté de X sur le plan de section.
 |
|
|
Il ne reste qu'a construire l'intersection Z de la droite (X'V') avec la génératrice définie par X, et ainsi on obtient l'intersection de la génératrice et le plan de section. |
CnkSect1.fig (la section dynamique d'un plan et d'un cone)
Contacter l'auteur de ces figures : Martin Acosta
Menu
général
